《2025年单元双测全优测评卷九年级数学下册苏科版》

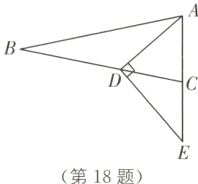
18.(2024·深圳中考)如图，在△ABC中，AB = BC，tan B = $\frac{5}{12}$. D为BC上一点，且满足$\frac{BD}{CD}$ = $\frac{8}{5}$，过点D作DE⊥AD交AC延长线于点E，则$\frac{CE}{AC}$ = ________.

答案： $\frac{20}{21}$ [解析]如图
(1)，过点A作AH⊥CB于点H，作CM⊥AD于点M，
∵AB = BC，$\frac{BD}{DC}$ = $\frac{8}{5}$，
∴设BD = 8a，则CD = 5a，
∴BC = AB = BD + CD = 13a.
∵tan B = $\frac{5}{12}$，
∴AH = 5a，BH = 12a，
∴DH = BH - BD = 4a，CH = a.
在Rt△ACH中，AC = $\sqrt{AH^{2}+CH^{2}}$ = $\sqrt{26}$a，
在Rt△ADH中，AD = $\sqrt{AH^{2}+DH^{2}}$ = $\sqrt{41}$a，
∴cos∠ADC = $\frac{DH}{AD}$ = $\frac{4\sqrt{41}}{41}$，
∴DM = CD·cos∠ADC = $\frac{20\sqrt{41}}{41}$a，
∴AM = AD - DM = $\frac{21\sqrt{41}}{41}$a.
∵CM⊥AD，DE⊥AD，
∴CM//DE，
∴△AMC∽△ADE，
∴$\frac{CE}{AC}$ = $\frac{DM}{AM}$ = $\frac{20}{21}$.

19.(8分)计算：
(1)sin²30° + sin 60° - sin²45° + cos²30°；
(2)$\frac{tan 30° + tan 45°}{tan 60°×tan 45°}$.

答案：
(1)原式 = ($\frac{1}{2}$)² + $\frac{\sqrt{3}}{2}$ - ($\frac{\sqrt{2}}{2}$)² + ($\frac{\sqrt{3}}{2}$)² = $\frac{1}{4}$ + $\frac{\sqrt{3}}{2}$ - $\frac{1}{2}$ + $\frac{3}{4}$ = $\frac{1+\sqrt{3}}{2}$.
(2)原式 = $\frac{\frac{\sqrt{3}}{3}+1}{\sqrt{3}×1}$ = $\frac{1+\sqrt{3}}{3}$.

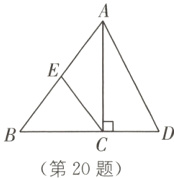
20.(6分)如图，在△ABD中，AC⊥BD于点C，$\frac{BC}{CD}$ = $\frac{3}{2}$，点E是AB的中点，tan D = 2，CE = 1，求sin∠ECB的值和AD的长.

答案：
∵AC⊥BD，
∴∠ACB = ∠ACD = 90°.
∵点E是AB的中点，CE = 1，
∴BE = CE = 1，AB = 2CE = 2，
∴∠B = ∠ECB.
∵$\frac{BC}{CD}$ = $\frac{3}{2}$，
∴设BC = 3x，CD = 2x.
在Rt△ACD中，tan D = 2，
∴$\frac{AC}{CD}$ = 2.
∴AC = 4x. 在Rt△ACB中，
由勾股定理，得AB = $\sqrt{AC^{2}+BC^{2}}$ = 5x.
∴sin∠ECB = sin B = $\frac{AC}{AB}$ = $\frac{4}{5}$.
由AB = 2，得x = $\frac{2}{5}$，
∴AD = $\sqrt{AC^{2}+CD^{2}}$ = $\sqrt{(4x)^{2}+(2x)^{2}}$ = 2$\sqrt{5}$x = 2$\sqrt{5}$×$\frac{2}{5}$ = $\frac{4\sqrt{5}}{5}$.