《2025年单元双测全优测评卷九年级数学下册苏科版》

26.(12分)原创素养题 逻辑推理 在△ABC与△A'B'C'中，点D与点D'分别在边BC、B'C'上，∠B = ∠B'，$\frac{BD}{BC}=\frac{B'D'}{B'C'}$.
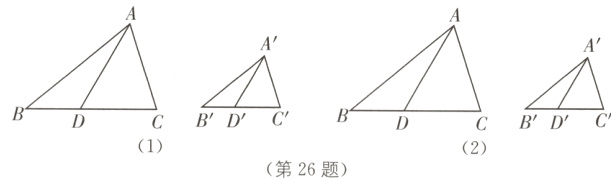
(1)如图(1)，当∠BAD = ∠B'A'D'时，求证：△ABC∽△A'B'C'.
(2)当∠CAD = ∠C'A'D'时，△ABC与△A'B'C'相似吗？小明发现：△ABC与△A'B'C'不一定相似. 小明先画出了△ABC∽△A'B'C'的示意图，如图(2)所示，请你利用无刻度的直尺和圆规在小明所画的图(2)中，作出△ABC与△A'B'C'不相似的反例.
(3)小明进一步探索：当∠B = ∠B' = 30°，∠CAD = ∠C'A'D' = 60°时，设$\frac{BD}{BC}=\frac{B'D'}{B'C'}=k(0＜k＜1)$，如果存在△ABC∽△A'B'C'，那么k的取值范围为_______.

答案：

(1)
∵∠B = ∠B',∠BAD = ∠B'A'D',
∴△ABD∽△A'B'D',
∴$\frac{BD}{B'D'}=\frac{AB}{A'B'}$.
∵$\frac{BD}{BC}=\frac{B'D'}{B'C'}$,
∴$\frac{BD}{B'D'}=\frac{BC}{B'C'}$,
∴$\frac{AB}{A'B'}=\frac{BC}{B'C'}$.
∵$\frac{AB}{A'B'}=\frac{BC}{B'C'}$,∠B = ∠B',
∴△ABC∽△A'B'C'.
(2)如图
(1),作△A'C'D'的外接圆交A'B'于点A'',连接A''D',则∠C'A''D' = ∠C'A'D'.

∵∠CAD = ∠C'A'D',
∴∠CAD = ∠C'A''D'.
但△ABC与△A''B'C'不相似,
故图
(1)中的△A''B'C'为所求作的反例.
(3)0＜k≤4 - 2$\sqrt{3}$ [解析]如图
(2),过点D作DE⊥AB于点E,DF⊥AC于点F,

由
(2)可得,当△ACD的外接圆与AB相切时,存在△ABC∽△A'B'C',此时易得∠C = ∠BAD,
又∠B = 30°,∠DAC = 60°,
∴∠BAD = ∠C = 45°,
此时$\frac{BD}{BC}$最大.
设DE = 1,
∴AD=$\sqrt{2}DE=\sqrt{2}$.
∵∠B = 30°,
∴BD = 2DE = 2.
在Rt△ADF中,∠DAC = 60°,
∴DF = AD·sin60°=$\sqrt{2}×\frac{\sqrt{3}}{2}=\frac{\sqrt{6}}{2}$.
在Rt△DCF中,∠C = 45°,
∴CD=$\sqrt{2}DF=\sqrt{3}$,
∴$\frac{BD}{BC}=\frac{2}{2+\sqrt{3}}=4 - 2\sqrt{3}$.
故k的取值范围是0＜k≤4 - 2$\sqrt{3}$.
解后反思 本题考查了相似三角形的判定和性质、确定圆的条件、解直角三角形等知识,解决问题的关键是熟练掌握“定弦对定角”等模型.