2025年单元双测全优测评卷九年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
23.(6分)某仓储中心有一个坡度为i = 1∶2的斜坡AB,顶部A处的高AC为4米,点B、C在同一水平地面上,其横截面如图所示.
(1)求该斜坡的坡面AB的长度;
(2)现有一个侧面图为矩形DEFG的长方体货柜,其中长DE = 2.5米,高EF = 2米,该货柜沿斜坡向上运送时,点D离BC所在水平面的高度不断变化,求当BF = 3.5米时,点D离BC所在水平面的高度DH.
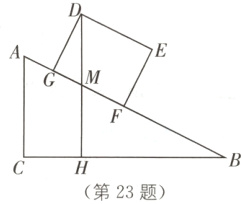
(1)求该斜坡的坡面AB的长度;
(2)现有一个侧面图为矩形DEFG的长方体货柜,其中长DE = 2.5米,高EF = 2米,该货柜沿斜坡向上运送时,点D离BC所在水平面的高度不断变化,求当BF = 3.5米时,点D离BC所在水平面的高度DH.

答案:
(1)
∵坡度为i = 1∶2,AC = 4米,
∴BC = 4×2 = 8(米).
∴AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{4^{2}+8^{2}}$ = 4$\sqrt{5}$(米).
(2)
∵∠DGM = ∠BHM = 90°,∠DMG = ∠BMH,
∴∠GDM = ∠B,
∴$\frac{GM}{GD}$ = $\frac{1}{2}$.
∵DG = EF = 2米,
∴GM = 1米,
∴DM = $\sqrt{1^{2}+2^{2}}$ = $\sqrt{5}$(米),BM = BF + FM = 3.5 + (2.5 - 1) = 5(米). 设MH = x米,则BH = 2x米,
∴x² + (2x)² = 5²,解得x = $\sqrt{5}$.
∴DH = $\sqrt{5}$ + $\sqrt{5}$ = 2$\sqrt{5}$(米).
(1)
∵坡度为i = 1∶2,AC = 4米,
∴BC = 4×2 = 8(米).
∴AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{4^{2}+8^{2}}$ = 4$\sqrt{5}$(米).
(2)
∵∠DGM = ∠BHM = 90°,∠DMG = ∠BMH,
∴∠GDM = ∠B,
∴$\frac{GM}{GD}$ = $\frac{1}{2}$.
∵DG = EF = 2米,
∴GM = 1米,
∴DM = $\sqrt{1^{2}+2^{2}}$ = $\sqrt{5}$(米),BM = BF + FM = 3.5 + (2.5 - 1) = 5(米). 设MH = x米,则BH = 2x米,
∴x² + (2x)² = 5²,解得x = $\sqrt{5}$.
∴DH = $\sqrt{5}$ + $\sqrt{5}$ = 2$\sqrt{5}$(米).
24.(6分)中考新考法 课题实践活动 在一次数学课外实践活动中,某小组要测量一幢大楼MN的高度,如图,在山坡的坡脚A处测得大楼顶部M的仰角是58°,沿着山坡向上走75米到达B处,在B处测得大楼顶部M的仰角是22°,已知斜坡AB的坡度i = 3∶4(坡度是指坡面的铅直高度与水平宽度的比),求大楼MN的高度.(图中的点A、B、M、N、C均在同一平面内,N、A、C在同一水平线上,参考数据:tan 22°≈0.4,tan 58°≈1.6)
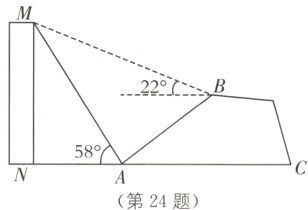

答案:
如图,过点B作BE⊥AC,垂足为E,过点B作BD⊥MN,垂足为D,则BE = DN,DB = NE.
∵斜坡AB的坡度i = 3∶4,
∴$\frac{BE}{AE}$ = $\frac{3}{4}$.
设BE = 3a米,则AE = 4a米.
在Rt△ABE中,AB = $\sqrt{AE^{2}+BE^{2}}$ = $\sqrt{(3a)^{2}+(4a)^{2}}$ = 5a(米),
∵AB = 75米,
∴5a = 75,
∴a = 15,
∴DN = BE = 45米,AE = 60米,
设NA = x米,则BD = NE = AN + AE = (x + 60)米.
在Rt△ANM中,∠NAM = 58°,
∴MN = AN·tan 58°≈1.6x(米),
∴DM = MN - DN = (1.6x - 45)米.
在Rt△MDB中,∠MBD = 22°,
∴tan 22° = $\frac{DM}{DB}$ = $\frac{1.6x - 45}{x + 60}$≈0.4,解得x = 57.5,
经检验,x = 57.5是原方程的解,
∴MN = 1.6x = 92(米),
∴大楼MN的高度约为92米.
∵斜坡AB的坡度i = 3∶4,
∴$\frac{BE}{AE}$ = $\frac{3}{4}$.
设BE = 3a米,则AE = 4a米.
在Rt△ABE中,AB = $\sqrt{AE^{2}+BE^{2}}$ = $\sqrt{(3a)^{2}+(4a)^{2}}$ = 5a(米),
∵AB = 75米,
∴5a = 75,
∴a = 15,
∴DN = BE = 45米,AE = 60米,
设NA = x米,则BD = NE = AN + AE = (x + 60)米.
在Rt△ANM中,∠NAM = 58°,
∴MN = AN·tan 58°≈1.6x(米),
∴DM = MN - DN = (1.6x - 45)米.
在Rt△MDB中,∠MBD = 22°,
∴tan 22° = $\frac{DM}{DB}$ = $\frac{1.6x - 45}{x + 60}$≈0.4,解得x = 57.5,
经检验,x = 57.5是原方程的解,
∴MN = 1.6x = 92(米),
∴大楼MN的高度约为92米.
查看更多完整答案,请扫码查看


