《2025年单元双测全优测评卷九年级数学下册苏科版》

23.(10分)原创素养题 应用意识 某校欲招聘一名数学教师，学校对甲、乙、丙三位候选人进行了三项能力测试，各项测试成绩满分均为100分，根据结果择优录用. 三位候选人的各项测试成绩如下表所示(单位：分)：

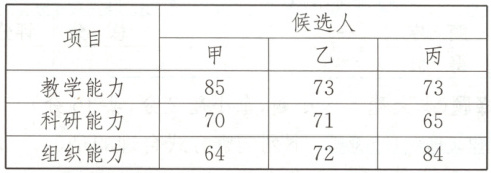
(1)如果根据三项测试的平均成绩，谁将被录用？说明理由.
(2)根据实际需要，学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩，谁将被录用？说明理由.

答案：
(1)候选人丙将被录用.理由如下：
甲的平均成绩：(85 + 70 + 64)÷3 = 73(分)；
乙的平均成绩：(73 + 71 + 72)÷3 = 72(分)；
丙的平均成绩：(73 + 65 + 84)÷3 = 74(分).
∵74＞73＞72，
∴候选人丙将被录用.
(2)候选人甲将被录用.理由如下：
甲的测试成绩为(85×5 + 70×3 + 64×2)÷(5 + 3 + 2)=76.3(分)；
乙的测试成绩为(73×5 + 71×3 + 72×2)÷(5 + 3 + 2)=72.2(分)；
丙的测试成绩为(73×5 + 65×3 + 84×2)÷(5 + 3 + 2)=72.8(分).
∵76.3＞72.8＞72.2，
∴候选人甲将被录用.

24.(12分)在四个完全相同的小球上，标注3、4、5这三个数字，每个小球上标一个数字. 把标注后的小球放进口袋中，从中随机拿出一个小球，已知$P$(一次拿到标4的球)=$\frac{1}{2}$.
(1)求这四个小球所标数字的中位数.
(2)拿出一个球并记录所标数字，剩下三个小球所标数字的众数没变，平均数变小.
①拿出的球上标的是哪个数字？请说明理由.
②在剩下的三个小球中，再随机拿出两个小球，先拿出一个小球并记录所标数字，不放回；再拿出一个小球并记录所标数字，用画树状图或列表法，求所记录的三个数字构成勾股数的概率.

答案：

(1)
∵四个小球中三个小球标注3、4、5这三个数字，已知P(一次拿到标4的球)=$\frac{1}{2}$，
∴第四个小球标注数字4，
∴这四个小球所标数字是3、4、4、5，
∴这四个数字的中位数是$\frac{4 + 4}{2}$=4.
(2)①拿出的球上标的数字是5.理由如下：
∵这四个小球所标数字的平均数是$\frac{1}{4}$×(3 + 4 + 4 + 5)=4，数字3、4、4、5的众数是4，数字3、4、4的平均数为$\frac{1}{3}$×(3 + 4 + 4)=$\frac{11}{3}$＜4，众数为4，
∴拿出的球上标的数字是5.
②画树状图如图
则共有6种等可能的结果：(5，3，4)，(5，3，4)，(5，4，3)，(5，4，4)，(5，4，3)，(5，4，4)，
构成勾股数的有4种等可能的结果：(5，3，4)，(5，3，4)，(5，4，3)，(5，4，3)，
∴所记录的三个数字构成勾股数的概率为$\frac{4}{6}$=$\frac{2}{3}$.