2025年单元双测全优测评卷九年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.(2023·泰州中考)在相同条件下的多次重复试验中,一个随机事件发生的频率为f,该事件的概率为P.下列说法正确的是( ).
A. 试验次数越多,f越大
B. f与P都可能发生变化
C. 试验次数越多,f越接近于P
D. 当试验次数很大时,f在P附近摆动,并趋于稳定
A. 试验次数越多,f越大
B. f与P都可能发生变化
C. 试验次数越多,f越接近于P
D. 当试验次数很大时,f在P附近摆动,并趋于稳定
答案:
D
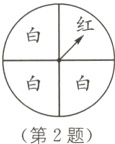
2.(2024·南京期末)如图,转盘中各个扇形的面积相等,任意转动转盘1次,当转盘停止转动时,指针指向白色区域的概率为( ).
A. $\frac{1}{4}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{3}{4}$

A. $\frac{1}{4}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{3}{4}$
答案:
D
3. 某斜坡的坡度i = 1:$\sqrt{3}$,则该斜坡的坡角为( ).
A. 75°
B. 60°
C. 45°
D. 30°
A. 75°
B. 60°
C. 45°
D. 30°
答案:
D
4. 若a:b = 4:3,且$b^{2}=ac$,则b:c等于( ).
A. 2:3
B. 3:2
C. 4:3
D. 3:4
A. 2:3
B. 3:2
C. 4:3
D. 3:4
答案:
C
5. 关于抛物线$y = x^{2}+2x - 3$,下列关于抛物线的说法正确的是( ).
A. 开口向下
B. 经过点(2,3)
C. 最低点的纵坐标是 - 3
D. 关于直线x = - 1对称
A. 开口向下
B. 经过点(2,3)
C. 最低点的纵坐标是 - 3
D. 关于直线x = - 1对称
答案:
D [解析]A. 由题意,得a = 1>0,所以抛物线的开口向上,故A错误;B. 当x = 2时,y = 2² + 2×2 - 3 = 4 + 4 - 3 = 5,所以图像经过(2,5),不经过(2,3),故B错误;C. 由题意,得y=(x + 1)² - 4,所以抛物线最低点的纵坐标是 - 4,故C错误;D. 由题意,得y=(x + 1)² - 4,所以抛物线的对称轴是直线x = -1,故D正确. 故选D.
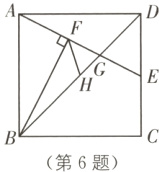
6.(2023·绥化中考)如图,在正方形ABCD中,点E为边CD的中点,连接AE,过点B作BF⊥AE于点F,连接BD交AE于点G,FH平分∠BFG交BD于点H.则下列结论中,正确的有( ).
①$AB^{2}=BF\cdot AE$;②$S_{\triangle BGF}$:$S_{\triangle BAF}=2$:3;③当AB = a时,$BD^{2}-BD\cdot HD=a^{2}$.
A. 0个
B. 1个
C. 2个
D. 3个
①$AB^{2}=BF\cdot AE$;②$S_{\triangle BGF}$:$S_{\triangle BAF}=2$:3;③当AB = a时,$BD^{2}-BD\cdot HD=a^{2}$.

A. 0个
B. 1个
C. 2个
D. 3个
答案:
D [解析]
∵四边形ABCD是正方形,
∴∠BAD = ∠ADE = 90°,AB = AD.
∵BF⊥AE,
∴∠ABF = 90° - ∠BAF = ∠EAD,
∴cos∠ABF = cos∠EAD,即$\frac{BF}{BA}=\frac{AD}{AE}$.
又AB = AD,
∴AB² = BF·AE. 故①正确;
设正方形的边长为a,
∵点E为边CD的中点,
∴DE=$\frac{a}{2}$,
∴tan∠ABF = tan∠EAD=$\frac{1}{2}$,
∴$\frac{AF}{BF}=\frac{1}{2}$,
∴BF = 2AF.
在Rt△ABF中,AB=$\sqrt{AF² + BF²}=\sqrt{5}AF = a$,
∴AF=$\frac{\sqrt{5}}{5}a$.
在Rt△ADE中,AE=$\sqrt{AD² + DE²}=\frac{\sqrt{5}}{2}a$.
∵AB//DE,
∴△GAB∽△GED,
∴$\frac{AG}{GE}=\frac{AB}{DE}=2$,
∴GE=$\frac{1}{3}AE=\frac{\sqrt{5}}{6}a$,
∴FG = AE - AF - GE=$\frac{\sqrt{5}}{2}a-\frac{\sqrt{5}}{5}a-\frac{\sqrt{5}}{6}a=\frac{2\sqrt{5}}{15}a$,
∴$\frac{AF}{FG}=\frac{\frac{\sqrt{5}}{5}a}{\frac{2\sqrt{5}}{15}a}=\frac{3}{2}$,
∴$S_{△BGF}:S_{△BAF}=2:3$. 故②正确;
∵AB = a,
∴AD = AB = a,
∴BD² = AB² + AD² = 2a²,
∴BD=$\sqrt{2}a$.
如图所示,过点H分别作BF、AE的垂线,垂足分别为M、N.

∵BF⊥AE,HM⊥BF,HN⊥AE,
∴四边形FMHN是矩形.
∵FH是∠BFG的平分线,
∴HM = HN,
∴四边形FMHN是正方形,
∴FN = HM = HN.
∵BF = 2AF=$\frac{2\sqrt{5}}{5}a$,FG=$\frac{2\sqrt{5}}{15}a$,
∴$\frac{MH}{BM}=\frac{FG}{BF}=\frac{1}{3}$.
设MH = b,则BM = 3b,BF = BM + FM = BM + MH = 3b + b = 4b,在Rt△BMH中,
BH=$\sqrt{BM² + MH²}=\sqrt{10}b$.
∵BF=$\frac{2\sqrt{5}}{5}a$,
∴$\frac{2\sqrt{5}}{5}a = 4b$,解得b=$\frac{\sqrt{5}}{10}a$.
∴BH=$\sqrt{10}×\frac{\sqrt{5}}{10}a=\frac{\sqrt{2}}{2}a$,HD = BD - BH=$\frac{\sqrt{2}}{2}a$,
∴BD² - BD·HD = 2a² - $\sqrt{2}a×\frac{\sqrt{2}}{2}a = a²$.
故③正确. 故选D.
D [解析]
∵四边形ABCD是正方形,
∴∠BAD = ∠ADE = 90°,AB = AD.
∵BF⊥AE,
∴∠ABF = 90° - ∠BAF = ∠EAD,
∴cos∠ABF = cos∠EAD,即$\frac{BF}{BA}=\frac{AD}{AE}$.
又AB = AD,
∴AB² = BF·AE. 故①正确;
设正方形的边长为a,
∵点E为边CD的中点,
∴DE=$\frac{a}{2}$,
∴tan∠ABF = tan∠EAD=$\frac{1}{2}$,
∴$\frac{AF}{BF}=\frac{1}{2}$,
∴BF = 2AF.
在Rt△ABF中,AB=$\sqrt{AF² + BF²}=\sqrt{5}AF = a$,
∴AF=$\frac{\sqrt{5}}{5}a$.
在Rt△ADE中,AE=$\sqrt{AD² + DE²}=\frac{\sqrt{5}}{2}a$.
∵AB//DE,
∴△GAB∽△GED,
∴$\frac{AG}{GE}=\frac{AB}{DE}=2$,
∴GE=$\frac{1}{3}AE=\frac{\sqrt{5}}{6}a$,
∴FG = AE - AF - GE=$\frac{\sqrt{5}}{2}a-\frac{\sqrt{5}}{5}a-\frac{\sqrt{5}}{6}a=\frac{2\sqrt{5}}{15}a$,
∴$\frac{AF}{FG}=\frac{\frac{\sqrt{5}}{5}a}{\frac{2\sqrt{5}}{15}a}=\frac{3}{2}$,
∴$S_{△BGF}:S_{△BAF}=2:3$. 故②正确;
∵AB = a,
∴AD = AB = a,
∴BD² = AB² + AD² = 2a²,
∴BD=$\sqrt{2}a$.
如图所示,过点H分别作BF、AE的垂线,垂足分别为M、N.

∵BF⊥AE,HM⊥BF,HN⊥AE,
∴四边形FMHN是矩形.
∵FH是∠BFG的平分线,
∴HM = HN,
∴四边形FMHN是正方形,
∴FN = HM = HN.
∵BF = 2AF=$\frac{2\sqrt{5}}{5}a$,FG=$\frac{2\sqrt{5}}{15}a$,
∴$\frac{MH}{BM}=\frac{FG}{BF}=\frac{1}{3}$.
设MH = b,则BM = 3b,BF = BM + FM = BM + MH = 3b + b = 4b,在Rt△BMH中,
BH=$\sqrt{BM² + MH²}=\sqrt{10}b$.
∵BF=$\frac{2\sqrt{5}}{5}a$,
∴$\frac{2\sqrt{5}}{5}a = 4b$,解得b=$\frac{\sqrt{5}}{10}a$.
∴BH=$\sqrt{10}×\frac{\sqrt{5}}{10}a=\frac{\sqrt{2}}{2}a$,HD = BD - BH=$\frac{\sqrt{2}}{2}a$,
∴BD² - BD·HD = 2a² - $\sqrt{2}a×\frac{\sqrt{2}}{2}a = a²$.
故③正确. 故选D.
查看更多完整答案,请扫码查看


