《2025年单元双测全优测评卷九年级数学下册苏科版》

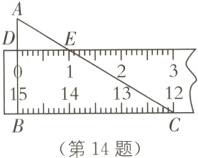
14. 如图，在△ABC中，∠ABC = 90°，∠A = 60°，直尺的一边与BC重合，另一边分别交AB、AC于点D、E. 点B、C、D、E处的读数分别为15、12、0、1，则直尺宽BD的长为_______.

答案： $\frac{2\sqrt{3}}{3}$　[解析]由题意，得DE = 1，BC = 3.
在Rt△ABC中，∠A = 60°，则AB = $\sqrt{3}$.
∵DE//BC，
∴△ADE∽△ABC，
∴$\frac{DE}{BC}=\frac{AD}{AB}$，即$\frac{1}{3}=\frac{\sqrt{3}-BD}{\sqrt{3}}$，解得BD = $\frac{2\sqrt{3}}{3}$.

15. 在△ABC中，D、E分别是AB、AC的中点，则三角形ADE与四边形DECB面积的比是_______.

答案： 1∶3　[解析]
∵D、E分别是AB、AC的中点，
∴DE//BC，
∴△ADE∽△ABC.
∵AD∶AB = 1∶2，
∴△ADE与△ABC的面积之比为1∶4，
∴三角形ADE与四边形DECB面积的比是1∶3.

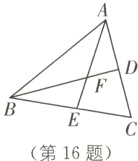
16. 如图，在△ABC中，D是AC的中点，△ABC的角平分线AE交BD于点F，若BF：FD = 3：1，AB + BE = 3$\sqrt{3}$，则△ABC的周长为_______.

答案：
$5\sqrt{3}$　[解析]如图，过点F作FM⊥AB交AB于点M，FN⊥AC交AC于点N，过点D作DT//AE交BC于点T.
∵AE平分∠BAC，FM⊥AB，FN⊥AC，
∴FM = FN，
∴$\frac{S_{\triangle ABF}}{S_{\triangle ADF}}=\frac{BF}{DF}=\frac{\frac{1}{2}AB\cdot FM}{\frac{1}{2}AD\cdot FN}=3$，
∴AB = 3AD.
设AD = DC = a，则AB = 3a.
∵AD = DC，DT//AE，
∴ET = CT，
∴$\frac{BE}{ET}=\frac{BF}{DF}=3$. 设ET = CT = b，则BE = 3b.
∵AB + BE = $3\sqrt{3}$，
∴3a + 3b = $3\sqrt{3}$，
∴a + b = $\sqrt{3}$.
∴△ABC的周长为AB + AC + BC = 5a + 5b = $5\sqrt{3}$.

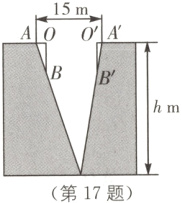
17. 如图是一个山谷的横截面示意图，宽AA′为15m，用曲尺(两直尺相交成直角)从山谷两侧测量出OA = 1m，OB = 3m，O′A′ = 0.5m，O′B′ = 3m(点A、O、O′、A′在同一条水平线上)，则该山谷的深h = _______m.

答案：
30　[解析]如图，设AB和A′B′相交于点D，过点D作DC垂直AA′于点C. A、A′到谷底的水平距离分别为AC = m，A′C = n，
∴m + n = 15 m.
根据题意，得OB//CD//O′B′.
∵OA = 1 m，OB = 3 m，O′A′ = 0.5 m，O′B′ = 3 m，
∴$\frac{h}{m}=\frac{OB}{OA}=3$，$\frac{h}{n}=\frac{O′B′}{O′A′}=6$，
∴m = $\frac{1}{3}h$，n = $\frac{1}{6}h$，
∴($\frac{1}{3}+\frac{1}{6}$)×h = 15，解得h = 30 m.

18. 在矩形ABCD中，由8个面积均为1的小正方形组成的L型模板按如图所示的方式放置，则矩形ABCD的周长为_______.

答案： 8$\sqrt{3}$

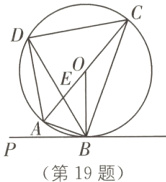
19.(6分)(2024·徐州模拟)如图，四边形ABCD内接于⊙O，AC是⊙O的直径，AC与BD交于点E，PB切⊙O于点B.
(1)求证：∠PBA = ∠OBC；
(2)若∠PBA = 20°，∠ACD = 40°，
求证：△OAB∽△CDE.

答案：
(1)
∵AC是⊙O的直径，
∴∠ABC = 90°.
∵PB切⊙O于点B，
∴∠PBO = 90°，
∴∠PBO - ∠ABO = ∠ABC - ∠ABO，
即∠PBA = ∠OBC.
(2)由
(1)知，∠PBA = ∠OBC = ∠ACB，
∵∠PBA = 20°，
∴∠OBC = ∠ACB = 20°，
∴∠AOB = ∠ACB + ∠OBC = 20° + 20° = 40°.
∵∠ACD = 40°，
∴∠AOB = ∠ACD.
∵$\overset{\frown}{BC}=\overset{\frown}{BC}$，
∴∠CDE = ∠BAO，
∴△OAB∽△CDE.

20.(6分)在如图所示的方格中，△OAB的顶点坐标分别为O(0，0)、A( - 2， - 1)、B( - 1， - 3)，△O₁A₁B₁与△OAB是关于点P为位似中心的位似图形.
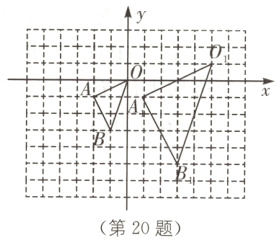
(1)在图中标出位似中心P的位置，并写出点P的坐标及△O₁A₁B₁与△OAB的相似比；
(2)以原点O为位似中心，在y轴的左侧画出△OAB的一个位似三角形△OA₂B₂，使它与△OAB的相似比为2：1，并写出点B的对应点B₂的坐标；
(3)在(2)的条件下，若点M(a，b)是△OAB边上一点(不与顶点重合)，写出点M在△OA₂B₂中的对应点M₂的坐标.

答案：

(1)点P的位置如图，点P的坐标为(-5，-1)，△O₁A₁B₁与△OAB的相似比为2∶1.
(2)如图，△OA₂B₂即为所求，点B₂的坐标为(-2，-6).

(3)点M₂的坐标为(2a，2b).