《2025年单元双测全优测评卷九年级数学下册苏科版》

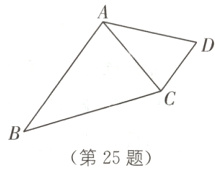
25.(8分)(2024·苏州立达中学期末)如图，四边形ABCD是某学校的一块种植实验基地，其中△ABC是水果园，△ACD是蔬菜园，已知AB//CD，AB = 27m，AC = 18m，CD = 12m.
(1)求证：△ABC∽△CAD；
(2)若蔬菜园△ACD的面积为80m²，求水果园△ABC的面积.

答案：
(1)
∵AB = 27 m，AC = 18 m，CD = 12 m，
∴$\frac{AB}{AC}=\frac{27}{18}=\frac{3}{2}$，$\frac{AC}{CD}=\frac{18}{12}=\frac{3}{2}$，
∴$\frac{AB}{AC}=\frac{AC}{CD}$.
∵AB//CD，
∴∠BAC = ∠ACD，
∴△ABC∽△CAD.
(2)由
(1)可知，△ABC∽△CAD，
∴$\frac{S_{\triangle ABC}}{S_{\triangle CAD}}=(\frac{3}{2})^{2}=\frac{9}{4}$.
∵△ACD的面积为80 m²，
∴△ABC的面积为80×$\frac{9}{4}$=180(m²).
故水果园△ABC的面积为180 m².

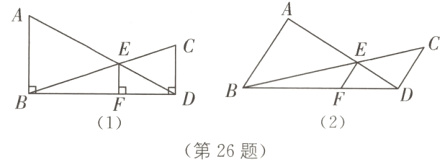
26.(8分)如图(1)，AB⊥BD，CD⊥BD，垂足分别为B、D，AD、BC相交于点E，过点E作EF⊥BD，则可以得到$\frac{1}{AB}+\frac{1}{CD}=\frac{1}{EF}$. 若将图(1)中的垂直改为斜交，如图(2)，AB//CD，AD、BC相交于点E，过点E作EF//AB交BD于点F，试问：
(1)$\frac{1}{AB}+\frac{1}{CD}=\frac{1}{EF}$还成立吗？请说明理由.
(2)试找出S△ABD、S△BED、S△BDC之间的数量关系，并说明理由.

答案：
(1)$\frac{1}{AB}+\frac{1}{CD}=\frac{1}{EF}$成立. 理由如下：
∵EF//AB//CD，
∴△DEF∽△DAB，△BEF∽△BCD，
∴$\frac{EF}{AB}=\frac{DF}{DB}$①，$\frac{EF}{CD}=\frac{BF}{BD}$②.
① + ②，得$\frac{EF}{AB}+\frac{EF}{CD}=\frac{DF}{DB}+\frac{BF}{BD}=1$，
故$\frac{1}{AB}+\frac{1}{CD}=\frac{1}{EF}$.
(2)$\frac{1}{S_{\triangle ABD}}+\frac{1}{S_{\triangle BCD}}=\frac{1}{S_{\triangle BED}}$. 理由如下：
过点A、E、C分别作BD的垂线，垂足为A′、E′、C′，
则$S_{\triangle ABD}=\frac{1}{2}BD\cdot AA′$，$S_{\triangle BED}=\frac{1}{2}BD\cdot EE′$，$S_{\triangle BCD}=\frac{1}{2}BD\cdot CC′$，
∴$\frac{S_{\triangle BED}}{S_{\triangle ABD}}=\frac{EE′}{AA′}$，$\frac{S_{\triangle BED}}{S_{\triangle BCD}}=\frac{EE′}{CC′}$.
由题意，可知$\frac{1}{AA′}+\frac{1}{CC′}=\frac{1}{EE′}$，
从而$\frac{1}{S_{\triangle ABD}}+\frac{1}{S_{\triangle BCD}}=\frac{1}{S_{\triangle BED}}$.