2025年单元双测全优测评卷九年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
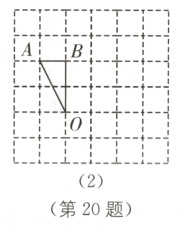
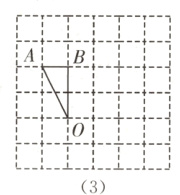
20. (6分)中考新考法 无刻度直尺作图(2023·常州模拟)如图,在6×6的正方形网格中,每个小正方形的边长均为1,且每个小正方形的顶点称为格点,△OAB的顶点均在格点上,按要求完成画图.(要求仅用无刻度的直尺,且保留必要的画图痕迹)
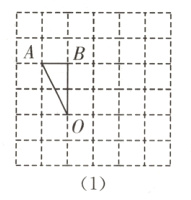
(1)在图(1)中,以BO为边,画出△OBC,使△OBC∽△ABO,C为格点;
(2)在图(2)中,以点O为位似中心. 画出△ODE,使△ODE与△OAB位似,且位似比$k = \frac{OD}{OA}=2$,点D、E为格点;
(3)在图(3)中,在边OA上找一个点F,且$\frac{AF}{OF}=3$满足.



(1)在图(1)中,以BO为边,画出△OBC,使△OBC∽△ABO,C为格点;
(2)在图(2)中,以点O为位似中心. 画出△ODE,使△ODE与△OAB位似,且位似比$k = \frac{OD}{OA}=2$,点D、E为格点;
(3)在图(3)中,在边OA上找一个点F,且$\frac{AF}{OF}=3$满足.
答案:
(1)如图
(1),△OBC即为所求.


(第20
(2)如图
(2),△ODE即为所求.
(3)如图
(3),取格点P、Q,连接PQ,交AO于点F,
则点F即为所求作的点.
∵△AQF∽△OPF,
∴$\frac{AF}{FO}=\frac{AQ}{OP}=3$.

(1)如图
(1),△OBC即为所求.


(第20
(2)如图
(2),△ODE即为所求.
(3)如图
(3),取格点P、Q,连接PQ,交AO于点F,
则点F即为所求作的点.
∵△AQF∽△OPF,
∴$\frac{AF}{FO}=\frac{AQ}{OP}=3$.

21. (6分)如图,在锐角三角形ABC中,点D、E分别在边AC、AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF = ∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD = 3,AB = 5,求$\frac{AF}{AG}$的值.
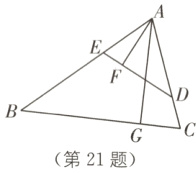
(1)求证:△ADE∽△ABC;
(2)若AD = 3,AB = 5,求$\frac{AF}{AG}$的值.

答案:
(1)
∵AG⊥BC,AF⊥DE,
∴∠AFE = ∠AGC = 90°.
∵∠EAF = ∠GAC,
∴∠AED = ∠ACB.
∵∠DAE = ∠BAC,
∴△ADE∽△ABC.
(2)
∵△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{AE}{AC}=\frac{3}{5}$.
∵∠AFE = ∠AGC = 90°,∠EAF = ∠CAG,
∴△EAF∽△CAG,
∴$\frac{AF}{AG}=\frac{AE}{AC}=\frac{3}{5}$.
(1)
∵AG⊥BC,AF⊥DE,
∴∠AFE = ∠AGC = 90°.
∵∠EAF = ∠GAC,
∴∠AED = ∠ACB.
∵∠DAE = ∠BAC,
∴△ADE∽△ABC.
(2)
∵△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{AE}{AC}=\frac{3}{5}$.
∵∠AFE = ∠AGC = 90°,∠EAF = ∠CAG,
∴△EAF∽△CAG,
∴$\frac{AF}{AG}=\frac{AE}{AC}=\frac{3}{5}$.
22. (6分)(2024·南京秦淮区二模)如图,在△ABC中,AB = AC,D、E分别是BC、AB上的点,且∠ADE = ∠C.
(1)求证:△ACD∽△DBE;
(2)求证:4BE·AC≤BC².
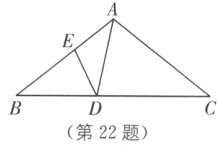
(1)求证:△ACD∽△DBE;
(2)求证:4BE·AC≤BC².

答案:
(1)
∵AB = AC,
∴∠B = ∠C.
∵∠BDA = ∠DAC + ∠C = ∠BDE + ∠ADE,∠ADE = ∠C,
∴∠BDE = ∠DAC,
∴△ACD∽△DBE.
(2)
∵△ACD∽△DBE,
∴$\frac{BE}{CD}=\frac{BD}{AC}$,即BE·AC = BD·CD,
设BC = m,BD = x,则CD = m - x,
∴4BE·AC = 4BD·CD = 4x(m - x)=-(2x - m)^{2}+m^{2},
∴4BE·AC≤m^{2},即4BE·AC≤BC^{2}.
(1)
∵AB = AC,
∴∠B = ∠C.
∵∠BDA = ∠DAC + ∠C = ∠BDE + ∠ADE,∠ADE = ∠C,
∴∠BDE = ∠DAC,
∴△ACD∽△DBE.
(2)
∵△ACD∽△DBE,
∴$\frac{BE}{CD}=\frac{BD}{AC}$,即BE·AC = BD·CD,
设BC = m,BD = x,则CD = m - x,
∴4BE·AC = 4BD·CD = 4x(m - x)=-(2x - m)^{2}+m^{2},
∴4BE·AC≤m^{2},即4BE·AC≤BC^{2}.
查看更多完整答案,请扫码查看


