《2025年单元双测全优测评卷九年级数学下册苏科版》

21.(6分)(2023·北京中考)在平面直角坐标系 $xOy$中，$M(x_{1},y_{1})$、$N(x_{2},y_{2})$是抛物线 $y = ax^{2}+bx + c(a＞0)$上任意两点，设抛物线的对称轴为直线 $x = t$.
(1)若对于 $x_{1}=1$，$x_{2}=2$，有 $y_{1}=y_{2}$，求 $t$的值；
(2)若对于 $0＜x_{1}＜1$，$1＜x_{2}＜2$，都有 $y_{1}＜y_{2}$，求 $t$的取值范围.

答案：
(1)
∵对于x₁ = 1，x₂ = 2，有y₁ = y₂，
∴a + b + c = 4a + 2b + c，
∴3a + b = 0，
∴$\frac{b}{a}$= - 3.
∵对称轴为x = -$\frac{b}{2a}$=$\frac{3}{2}$，
∴t = $\frac{3}{2}$.
(2)
∵0＜x₁＜1，1＜x₂＜2，
∴$\frac{1}{2}$＜$\frac{x₁ + x₂}{2}$＜$\frac{3}{2}$，
x₁＜x₂.
∵y₁＜y₂，a＞0，
∴(x₁,y₁)离对称轴更近，x₁＜x₂，则(x₁,y₁)与(x₂,y₂)的中点在对称轴的右侧，
∴$\frac{x₁ + x₂}{2}$＞t，即t≤$\frac{1}{2}$.

22.(6分)(2023·牡丹江中考)如图，抛物线 $y = x^{2}+bx + c$与 $x$轴交于点 $A( - 1,0)$、$B(4,0)$，与 $y$轴交于点 $C$.
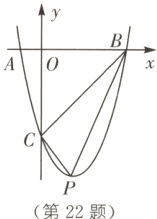
(1)求抛物线对应的函数表达式，并直接写出顶点 $P$的坐标；
(2)求$\triangle BCP$的面积.

答案：

(1)
∵抛物线y = x² + bx + c与x轴交于点A(-1,0)，B(4,0)，
∴$\begin{cases}1 - b + c = 0 \\16 + 4b + c = 0\end{cases}$，解得$\begin{cases}b = - 3 \\c = - 4\end{cases}$.
∴抛物线的表达式为y = x² - 3x - 4，
即y = (x - $\frac{3}{2}$)² - $\frac{25}{4}$，
∴P($\frac{3}{2}$,-$\frac{25}{4}$).
(2)如图，连接OP.

∵A(-1,0)，B(4,0)，C(0,-4)，P($\frac{3}{2}$,-$\frac{25}{4}$).
∴S_{△OPC}=$\frac{1}{2}$×4×$\frac{3}{2}$=3，S_{△BOP}=$\frac{1}{2}$×4×$\frac{25}{4}$=$\frac{25}{2}$，S_{△BOC}=$\frac{1}{2}$×4×4 = 8，
∴S_{△BPC}=S_{△OPC}+S_{△BOP}-S_{△BOC}=3+$\frac{25}{2}$-8=$\frac{15}{2}$.