第97页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. 定义:一次函数$y = ax + b$和一次函数$y = -bx - a$为“逆反函数”,如$y = 3x + 2$和$y = -2x - 3$为“逆反函数”. 若点$A(a,3)$在$y = x + 2$的“逆反函数”的图象上,则$a =$______.
答案:
-2
2. 定义:对于给定的一次函数$y = ax + b(a\neq0)$,把形如$y=\begin{cases}ax + b(x\geq0)\\-ax + b(x<0)\end{cases}$的函数称为一次函数$y = ax + b$的衍生函数. 已知函数$y = 2x + 1$,若点$P(1,m)$,$Q(-1,n)$在这个一次函数的衍生函数图象上,则$m =$______,$n =$______.
答案:
3;3
3. 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫常态三角形. 例如:一个三角形的三边长分别是5,6和8,因为$6^{2}+8^{2}=4\times5^{2}=100$,所以这个三角形是常态三角形.
(1) 若$\triangle ABC$的三边长分别是$2,\sqrt{5}$和4,则此三角形______常态三角形(填“是”或“不是”).
(2) 若$Rt\triangle ABC$是常态三角形,则此三角形的三边长之比为____________(从小到大排列).
(3) 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$BC = 6$,$CD = AD = DB$,若$\triangle BCD$是常态三角形,求$\triangle ABC$的面积.

(1) 若$\triangle ABC$的三边长分别是$2,\sqrt{5}$和4,则此三角形______常态三角形(填“是”或“不是”).
(2) 若$Rt\triangle ABC$是常态三角形,则此三角形的三边长之比为____________(从小到大排列).
(3) 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$BC = 6$,$CD = AD = DB$,若$\triangle BCD$是常态三角形,求$\triangle ABC$的面积.

答案:
(1) 是。
(2) $\sqrt{2}:\sqrt{3}:\sqrt{5}$。
(3) 设 $CD = x(x>0)$,则 $AD = BD = CD = x$,$AB = 2x$。因为 $\triangle BCD$ 是常态三角形,所以有以下两种可能。 ①当 $x^{2}+x^{2}=4BC^{2}=4\times6^{2}=144$ 时,$x^{2}=72$,所以 $x = 6\sqrt{2}$,所以 $AB = 12\sqrt{2}$,由勾股定理得 $AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{288 - 36}=6\sqrt{7}$,则 $S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}\times6\sqrt{7}\times6 = 18\sqrt{7}$。 ②当 $x^{2}+6^{2}=4x^{2}$ 时,$x^{2}=12$,所以 $x = 2\sqrt{3}$,所以 $AB = 4\sqrt{3}$,由勾股定理得 $AC=\sqrt{(4\sqrt{3})^{2}-6^{2}}=\sqrt{12}=2\sqrt{3}$,则 $S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}\times2\sqrt{3}\times6 = 6\sqrt{3}$。 综上,$\triangle ABC$ 的面积为 $6\sqrt{3}$ 或 $18\sqrt{7}$。
(1) 是。
(2) $\sqrt{2}:\sqrt{3}:\sqrt{5}$。
(3) 设 $CD = x(x>0)$,则 $AD = BD = CD = x$,$AB = 2x$。因为 $\triangle BCD$ 是常态三角形,所以有以下两种可能。 ①当 $x^{2}+x^{2}=4BC^{2}=4\times6^{2}=144$ 时,$x^{2}=72$,所以 $x = 6\sqrt{2}$,所以 $AB = 12\sqrt{2}$,由勾股定理得 $AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{288 - 36}=6\sqrt{7}$,则 $S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}\times6\sqrt{7}\times6 = 18\sqrt{7}$。 ②当 $x^{2}+6^{2}=4x^{2}$ 时,$x^{2}=12$,所以 $x = 2\sqrt{3}$,所以 $AB = 4\sqrt{3}$,由勾股定理得 $AC=\sqrt{(4\sqrt{3})^{2}-6^{2}}=\sqrt{12}=2\sqrt{3}$,则 $S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}\times2\sqrt{3}\times6 = 6\sqrt{3}$。 综上,$\triangle ABC$ 的面积为 $6\sqrt{3}$ 或 $18\sqrt{7}$。
4. 定义:若一个四边形的四条边和两条对角线这六条线段中只有两种长度,则我们把这样的四边形叫做双距四边形.
(1) 下列说法正确的有______(填序号).
①正方形一定是双距四边形;
②矩形一定是双距四边形;
③有一个内角为$60^{\circ}$的菱形是双距四边形.
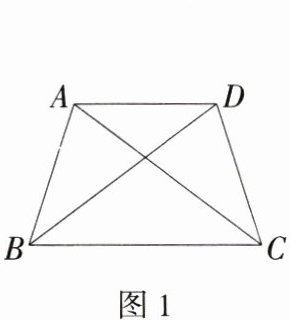
(2) 如图1,在四边形$ABCD$中,$AD// BC$,$AB = AD$,$\angle ABC = \angle DCB = 72^{\circ}$,求证:四边形$ABCD$为双距四边形.
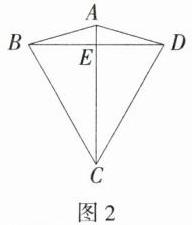
(3) 如图2,四边形$ABCD$为双距四边形,$AB = AD=\sqrt{6}$,$BC = DC$,$AB<BC$,求$BC$的长.

(1) 下列说法正确的有______(填序号).
①正方形一定是双距四边形;
②矩形一定是双距四边形;
③有一个内角为$60^{\circ}$的菱形是双距四边形.
(2) 如图1,在四边形$ABCD$中,$AD// BC$,$AB = AD$,$\angle ABC = \angle DCB = 72^{\circ}$,求证:四边形$ABCD$为双距四边形.
(3) 如图2,四边形$ABCD$为双距四边形,$AB = AD=\sqrt{6}$,$BC = DC$,$AB<BC$,求$BC$的长.


答案:
(1) 因为正方形的四条边都相等,两条对角线相等,所以正方形的四条边和两条对角线这六条线段中只有两种长度,所以正方形是双距四边形,故①正确;因为矩形的两组对边分别相等,两条对角线相等,所以矩形的四条边和两条对角线这六条线段中可能有三种长度,所以矩形不一定是双距四边形,故②错误;因为菱形的四条边都相等,且有一个内角为 $60^{\circ}$,所以该菱形中较短的对角线将该菱形分成两个全等的等边三角形,所以该菱形中较短的对角线长与该菱形的边长相等,所以有一个内角为 $60^{\circ}$ 的菱形的四条边和两条对角线这六条线段中只有两种长度,所以有一个内角为 $60^{\circ}$ 的菱形是双距四边形,故③正确。故答案为①③。
(2) 证明:作 $DG// AB$ 交 $BC$ 于点 $G$,如图 1。因为 $\angle ABC=\angle DCB = 72^{\circ}$,$DG// AB$,所以 $\angle DGC=\angle ABC = 72^{\circ}=\angle DCB$,所以 $DC = DG$。因为 $AD// BC$,所以四边形 $ABGD$ 是平行四边形,所以 $AB = DG$,所以 $AB = DC$。因为 $AB = AD$,所以 $AB = AD = DC$,$\angle ADB=\angle ABD$。因为 $AD// BC$,所以 $\angle ADB=\angle CBD$,$\angle CDA = 180^{\circ}-\angle DCB = 108^{\circ}$,所以 $\angle ADB=\angle ABD=\angle CBD=\frac{1}{2}\angle ABC = 36^{\circ}$,所以 $\angle CDB=\angle CDA-\angle ADB = 72^{\circ}=\angle DCB$,所以 $BC = BD$。在 $\triangle ABC$ 和 $\triangle DCB$ 中,$\begin{cases}AB = DC\\\angle ABC=\angle DCB\\BC = CB\end{cases}$,所以 $\triangle ABC\cong\triangle DCB(SAS)$,所以 $AC = BD$,所以 $AC = BC = BD$,所以四边形 $ABCD$ 是双距四边形。
(3) 如图 2,设 $AC$ 交 $BD$ 于点 $E$。因为四边形 $ABCD$ 为双距四边形,$AB = AD$,$BC = DC$,$AB<BC$,所以 $AC = BD = BC = DC$,设 $AC = BD = BC = 2x$,易知点 $A$、点 $C$ 都在 $BD$ 的垂直平分线上,所以 $AC$ 垂直平分 $BD$,所以 $\angle AEB=\angle CEB = 90^{\circ}$,$BE = DE=\frac{1}{2}BD=\frac{1}{2}BC = x$,所以 $CE=\sqrt{BC^{2}-BE^{2}}=\sqrt{(2x)^{2}-x^{2}}=\sqrt{3}x$,所以 $AE = AC - CE = 2x-\sqrt{3}x$。因为 $BE^{2}+AE^{2}=AB^{2}$,$AB=\sqrt{6}$,所以 $x^{2}+(2x-\sqrt{3}x)^{2}=(\sqrt{6})^{2}$,整理得 $x^{2}=(\frac{3 + \sqrt{3}}{2})^{2}$,解得 $x=\frac{3+\sqrt{3}}{2}$ 或 $x=-\frac{3+\sqrt{3}}{2}$(不符合题意,舍去),所以 $BC = 2\times\frac{3+\sqrt{3}}{2}=3+\sqrt{3}$。

(1) 因为正方形的四条边都相等,两条对角线相等,所以正方形的四条边和两条对角线这六条线段中只有两种长度,所以正方形是双距四边形,故①正确;因为矩形的两组对边分别相等,两条对角线相等,所以矩形的四条边和两条对角线这六条线段中可能有三种长度,所以矩形不一定是双距四边形,故②错误;因为菱形的四条边都相等,且有一个内角为 $60^{\circ}$,所以该菱形中较短的对角线将该菱形分成两个全等的等边三角形,所以该菱形中较短的对角线长与该菱形的边长相等,所以有一个内角为 $60^{\circ}$ 的菱形的四条边和两条对角线这六条线段中只有两种长度,所以有一个内角为 $60^{\circ}$ 的菱形是双距四边形,故③正确。故答案为①③。
(2) 证明:作 $DG// AB$ 交 $BC$ 于点 $G$,如图 1。因为 $\angle ABC=\angle DCB = 72^{\circ}$,$DG// AB$,所以 $\angle DGC=\angle ABC = 72^{\circ}=\angle DCB$,所以 $DC = DG$。因为 $AD// BC$,所以四边形 $ABGD$ 是平行四边形,所以 $AB = DG$,所以 $AB = DC$。因为 $AB = AD$,所以 $AB = AD = DC$,$\angle ADB=\angle ABD$。因为 $AD// BC$,所以 $\angle ADB=\angle CBD$,$\angle CDA = 180^{\circ}-\angle DCB = 108^{\circ}$,所以 $\angle ADB=\angle ABD=\angle CBD=\frac{1}{2}\angle ABC = 36^{\circ}$,所以 $\angle CDB=\angle CDA-\angle ADB = 72^{\circ}=\angle DCB$,所以 $BC = BD$。在 $\triangle ABC$ 和 $\triangle DCB$ 中,$\begin{cases}AB = DC\\\angle ABC=\angle DCB\\BC = CB\end{cases}$,所以 $\triangle ABC\cong\triangle DCB(SAS)$,所以 $AC = BD$,所以 $AC = BC = BD$,所以四边形 $ABCD$ 是双距四边形。
(3) 如图 2,设 $AC$ 交 $BD$ 于点 $E$。因为四边形 $ABCD$ 为双距四边形,$AB = AD$,$BC = DC$,$AB<BC$,所以 $AC = BD = BC = DC$,设 $AC = BD = BC = 2x$,易知点 $A$、点 $C$ 都在 $BD$ 的垂直平分线上,所以 $AC$ 垂直平分 $BD$,所以 $\angle AEB=\angle CEB = 90^{\circ}$,$BE = DE=\frac{1}{2}BD=\frac{1}{2}BC = x$,所以 $CE=\sqrt{BC^{2}-BE^{2}}=\sqrt{(2x)^{2}-x^{2}}=\sqrt{3}x$,所以 $AE = AC - CE = 2x-\sqrt{3}x$。因为 $BE^{2}+AE^{2}=AB^{2}$,$AB=\sqrt{6}$,所以 $x^{2}+(2x-\sqrt{3}x)^{2}=(\sqrt{6})^{2}$,整理得 $x^{2}=(\frac{3 + \sqrt{3}}{2})^{2}$,解得 $x=\frac{3+\sqrt{3}}{2}$ 或 $x=-\frac{3+\sqrt{3}}{2}$(不符合题意,舍去),所以 $BC = 2\times\frac{3+\sqrt{3}}{2}=3+\sqrt{3}$。


查看更多完整答案,请扫码查看


