《2025年5年中考3年模拟八年级数学下册人教版》

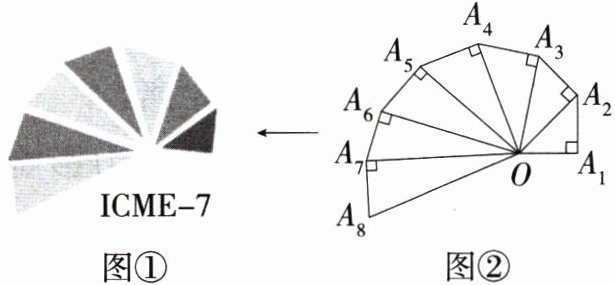
11.图①是第七届国际数学教育大会(ICME - 7)的会徽图案,它是由一串有公共顶点的直角三角形演化而成的.如图②,若$OA_{1}=A_{1}A_{2}=A_{2}A_{3}=\cdots=A_{7}A_{8}=2$,则$OA_{8}$的长是________.

答案： 答案：$4\sqrt{2}$ 解析：$\because OA_{1}=A_{1}A_{2}=A_{2}A_{3}=\cdots=A_{7}A_{8}=2$，$\therefore$ 由勾股定理可得 $OA_{2}=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$，$OA_{3}=\sqrt{(2\sqrt{2})^{2}+2^{2}} = 2\sqrt{3}$，$\cdots\cdots$，$\therefore OA_{n}=2\sqrt{n}$，$\therefore OA_{8}=2\sqrt{8}=4\sqrt{2}$。

12.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.以格点为顶点画三角形,使三角形的三边长分别为3,$2\sqrt{2}$,$\sqrt{5}$.

答案：
解析：由于 $(2\sqrt{2})^{2}=8 = 2^{2}+2^{2}$，因此可以构造一个两条直角边长均为 $2$ 的直角三角形，这个直角三角形的斜边长就是 $2\sqrt{2}$。要构造一条长度为 $\sqrt{5}$ 的线段，可构造一个直角边长分别为 $2$ 和 $1$ 的直角三角形，然后通过平移线段得到三角形。如图所示，$\triangle ABC$ 即为所求作的三角形。（所作三角形的形状和大小是唯一确定的，可画在不同位置）

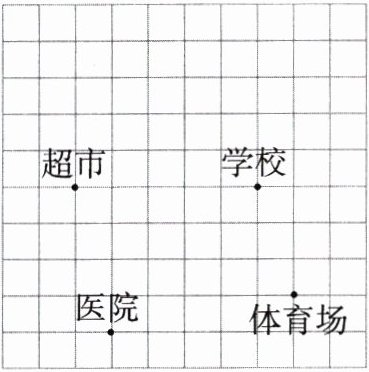
13.(2022浙江金华中考,7,★☆☆)如图所示的是城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是(3,1),(4,-2),下列各地点中,离原点最近的是 （ ）

A.超市
B.医院
C.体育场
D.学校

答案：
A 如图所示，点 $O$ 到超市的距离为 $\sqrt{2^{2}+1^{2}}=\sqrt{5}$，点 $O$ 到学校的距离为 $\sqrt{3^{2}+1^{2}}=\sqrt{10}$，点 $O$ 到体育场的距离为 $\sqrt{4^{2}+2^{2}} = 2\sqrt{5}$，点 $O$ 到医院的距离为 $\sqrt{1^{2}+3^{2}}=\sqrt{10}$，$\because\sqrt{5}＜\sqrt{10}＜2\sqrt{5}$，$\therefore$ 点 $O$ 到超市的距离最近，故选 A。

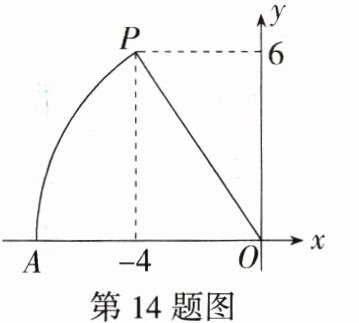
14.(2023山东临沂期中,2,★☆☆)如图,在平面直角坐标系中,点P的坐标为(-4,6),以点O为圆心,OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于 （ ）

A.-8和-7之间
B.7和8之间
C.-9和-8之间
D.8和9之间

答案： A $\because$ 点 $P$ 的坐标为 $( - 4,6)$，$\therefore OP=\sqrt{4^{2}+6^{2}}=\sqrt{52}$，由作图可知 $OA = OP=\sqrt{52}$，$\because 49＜52＜64$，$\therefore 7＜\sqrt{52}＜8$。$\because$ 点 $A$ 在 $x$ 轴的负半轴上，$\therefore$ 点 $A$ 的横坐标介于 $- 8$ 和 $- 7$ 之间，故选 A。

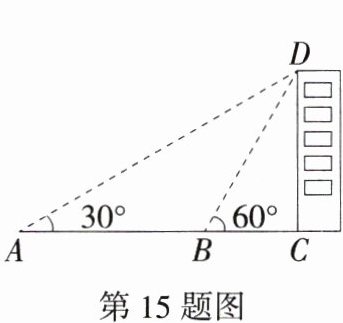
15.(2024四川雅安中考,11,★★☆)在数学课外实践活动中,某小组测量一栋楼房CD的高度(如图),他们在A处仰望楼顶,测得仰角∠A = 30°,再往楼的方向前进50米至B处,测得仰角∠DBC = 60°,那么这栋楼的高度为(人的身高忽略不计)(M8217001) （ ）

A.25$\sqrt{3}$米
B.25米
C.25$\sqrt{2}$米
D.50米

答案： A 设 $CD = x$ 米，在 $Rt\triangle ACD$ 中，$\angle A = 30^{\circ}$，$\therefore AD = 2CD = 2x$ 米，根据勾股定理，得 $AC=\sqrt{AD^{2}-CD^{2}}=\sqrt{(2x)^{2}-x^{2}}=\sqrt{3}x$ 米，在 $Rt\triangle BCD$ 中，$\angle DBC = 60^{\circ}$，$\therefore\angle BDC = 30^{\circ}$，$\therefore BD = 2BC$，根据勾股定理，得 $BC^{2}+CD^{2}=BD^{2}$，即 $BC^{2}+x^{2}=4BC^{2}$，整理得 $BC=\frac{\sqrt{3}}{3}x$ 米，$\because AB = AC - BC = 50$ 米，$\therefore\sqrt{3}x-\frac{\sqrt{3}}{3}x = 50$，解得 $x = 25\sqrt{3}$，$\therefore$ 这栋楼的高度为 $25\sqrt{3}$ 米，故选 A。

16.跨语文·诗词 (2024吉林中考,13,★★☆)图①中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图②,其中AB = AB',AB⊥B'C于点C,BC = 0.5尺,B'C = 2尺.设AC的长度为x尺,可列方程为________________.

答案： 答案：$x^{2}+2^{2}=(x + 0.5)^{2}$ 解析：$\because AC = x$ 尺，$\therefore AB'=AB=(x + 0.5)$ 尺，在 $Rt\triangle AB'C$ 中，由勾股定理得 $AC^{2}+B'C^{2}=AB'^{2}$，即 $x^{2}+2^{2}=(x + 0.5)^{2}$。

17.(2024陕西西安西北工大附中期末,15,★★☆)如图,在数轴上,点A、B表示的数分别为0、2,BC⊥AB于点B,且BC = 1,连接AC,在AC上截取CD = BC,以A为圆心,AD的长为半径画弧,交线段AB于点E,则点E表示的实数是________.

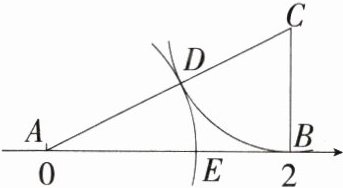
答案： 答案：$\sqrt{5}-1$ 解析：在 $Rt\triangle ABC$ 中，$BC = 1$，$AB = 2$，$\therefore AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{2^{2}+1^{2}}=\sqrt{5}$，$\because CD = BC = 1$，$\therefore AD = AC - CD=\sqrt{5}-1$，$\therefore AE = AD=\sqrt{5}-1$，$\therefore$ 点 $E$ 表示的实数是 $\sqrt{5}-1$。