第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
9.如图所示的是某中学教学楼楼梯侧面图,楼梯扶手下的玻璃为平行四边形.小友课间用量角器量得∠D = 60°,已知AB = 2.5 m,BC = 1.2 m,则这块玻璃的面积为________ m².


答案:
答案 $\frac{3\sqrt{3}}{2}$ 解析 如图,过点C作CE⊥AB于点E,
因为四边形ABCD是平行四边形,所以∠B = ∠D = 60°,所以∠BCE = 90° - 60° = 30°。因为BC = 1.2 m,所以BE = $\frac{1}{2}BC = 0.6$ m。根据勾股定理,得CE = $\sqrt{BC^{2}-BE^{2}}=\sqrt{1.2^{2}-0.6^{2}}=\frac{3\sqrt{3}}{5}(m)$,所以$S_{平行四边形ABCD}=AB\cdot CE = 2.5\times\frac{3\sqrt{3}}{5}=\frac{3\sqrt{3}}{2}(m^{2})$。
答案 $\frac{3\sqrt{3}}{2}$ 解析 如图,过点C作CE⊥AB于点E,

因为四边形ABCD是平行四边形,所以∠B = ∠D = 60°,所以∠BCE = 90° - 60° = 30°。因为BC = 1.2 m,所以BE = $\frac{1}{2}BC = 0.6$ m。根据勾股定理,得CE = $\sqrt{BC^{2}-BE^{2}}=\sqrt{1.2^{2}-0.6^{2}}=\frac{3\sqrt{3}}{5}(m)$,所以$S_{平行四边形ABCD}=AB\cdot CE = 2.5\times\frac{3\sqrt{3}}{5}=\frac{3\sqrt{3}}{2}(m^{2})$。
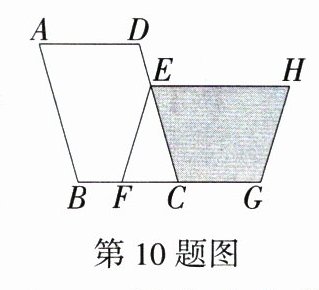
10.(2024台湾省中考,18,★★☆)如图,平行四边形ABCD与平行四边形EFGH全等,且A、B、C、D的对应顶点分别是H、E、F、G,其中E在DC上,F在BC上,C在FG上.若AB = 7,AD = 5,FC = 3,则四边形ECGH的周长为(M8218001) ( )
A.21
B.20
C.19
D.18

A.21
B.20
C.19
D.18
答案:
A 因为平行四边形ABCD与平行四边形EFGH全等,所以AB = CD = HE = FG = 7,AD = HG = EF = 5,∠DCB = ∠GFE,所以EC = EF = 5,因为FC = 3,所以CG = FG - FC = 4,所以四边形ECGH的周长 = EC + CG + HG + EH = 5 + 4 + 5 + 7 = 21,故选A。
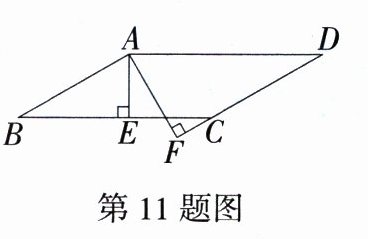
11.(2024河南南阳期末改编,7,★★☆)如图,在□ABCD中,AE⊥BC于点E,AF⊥CD交DC的延长线于点F.若AE = 2,AF = 3,且□ABCD的周长为20,则□ABCD的面积为 ( )
A.8
B.12
C.16
D.24

A.8
B.12
C.16
D.24
答案:
B 因为四边形ABCD是平行四边形,所以AD = BC,AB = CD,因为□ABCD的周长为20,所以2(BC + CD)=20,所以BC + CD = 10,因为AE⊥BC,AF⊥CD,所以$S_{□ABCD}=BC\cdot AE = CD\cdot AF$,因为AE = 2,AF = 3,所以2BC = 3CD,所以BC = $\frac{3}{2}CD$,所以$\frac{3}{2}CD + CD = 10$,所以CD = 4,所以$S_{□ABCD}=CD\cdot AF = 4\times3 = 12$,故选B。
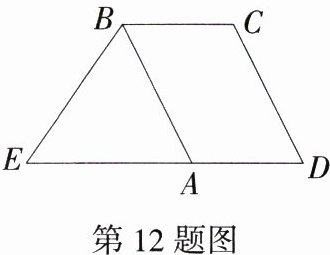
12.(2024广东广州中考,13,★★☆)如图,□ABCD中,BC = 2,点E在DA的延长线上,BE = 3,若BA平分∠EBC,则DE = ________.

答案:
答案 5
解析 因为四边形ABCD是平行四边形,所以AD//BC,AD = BC = 2,所以∠EAB = ∠CBA,因为BA平分∠EBC,所以∠EBA = ∠CBA,所以∠EAB = ∠EBA,所以AE = BE = 3,所以DE = AD + AE = 2 + 3 = 5。
13.(2023四川凉山州中考,15,★★☆)如图,□ABCO的顶点O、A、C的坐标分别是(0,0)、(3,0)、(1,2),则顶点B的坐标是________.


答案:
答案 (4,2) 解析 如图,延长BC交y轴于点D,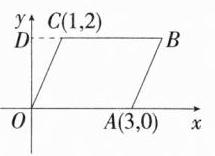
因为四边形ABCO是平行四边形,所以BC = OA,BC//OA,因为OA⊥y轴,所以BC⊥y轴,因为A(3,0),C(1,2),所以BC = OA = 3,CD = 1,OD = 2,所以BD = CD + BC = 1 + 3 = 4,所以B(4,2)。
答案 (4,2) 解析 如图,延长BC交y轴于点D,

因为四边形ABCO是平行四边形,所以BC = OA,BC//OA,因为OA⊥y轴,所以BC⊥y轴,因为A(3,0),C(1,2),所以BC = OA = 3,CD = 1,OD = 2,所以BD = CD + BC = 1 + 3 = 4,所以B(4,2)。
1.[已知一个内角的平分线](2023湖南株洲中考)如图所示,在平行四边形ABCD中,AB = 5,AD = 3,∠DAB的平分线AE交线段CD于点E,则EC = ________.
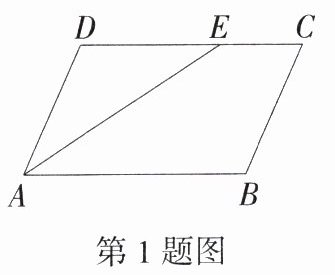

答案:
答案 2
解析 因为四边形ABCD是平行四边形,所以AB//CD,CD = AB = 5,所以∠BAE = ∠DEA,因为AE平分∠BAD,所以∠DAE = ∠BAE,所以∠DAE = ∠DEA,所以DE = AD = 3,所以EC = CD - DE = 5 - 3 = 2。
2.[已知两个内角的平分线]如图,在□ABCD中,BE平分∠ABC交AD于点E,CF平分∠BCD交AD于点F.若AB = 5,BC = 9,则EF的长为________.


答案:
答案 1
解析 因为四边形ABCD是平行四边形,所以AD//BC,所以∠AEB = ∠EBC,因为BE平分∠ABC,所以∠ABE = ∠EBC,所以∠ABE = ∠AEB,所以AE = AB = 5,同理可证DF = DC = AB = 5,因为AD = BC = 9,所以EF = AE + FD - AD = 5 + 5 - 9 = 1。
3.[已知内角的平分线与一边延长线相交](2023湖南长沙中考)如图,在□ABCD中,DF平分∠ADC,交BC于点E,交AB的延长线于点F.
(1)求证:AD = AF.
(2)若AD = 6,AB = 3,∠A = 120°,求BF的长和△ADF的面积.
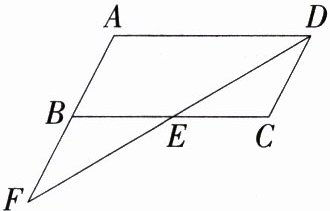
(1)求证:AD = AF.
(2)若AD = 6,AB = 3,∠A = 120°,求BF的长和△ADF的面积.

答案:
解析
(1)证明:在□ABCD中,AB//CD,所以∠CDE = ∠F,因为DF平分∠ADC,所以∠ADE = ∠CDE,所以∠F = ∠ADF,所以AD = AF。
(2)因为AD = AF = 6,AB = 3,所以BF = AF - AB = 3。过D作DH⊥AF交FA的延长线于H,如图,
因为∠BAD = 120°,所以∠DAH = 60°,所以∠ADH = 30°,所以AH = $\frac{1}{2}AD = 3$,所以DH = $\sqrt{AD^{2}-AH^{2}} = 3\sqrt{3}$,所以△ADF的面积 = $\frac{1}{2}AF\cdot DH=\frac{1}{2}\times6\times3\sqrt{3}=9\sqrt{3}$。
解析
(1)证明:在□ABCD中,AB//CD,所以∠CDE = ∠F,因为DF平分∠ADC,所以∠ADE = ∠CDE,所以∠F = ∠ADF,所以AD = AF。
(2)因为AD = AF = 6,AB = 3,所以BF = AF - AB = 3。过D作DH⊥AF交FA的延长线于H,如图,

因为∠BAD = 120°,所以∠DAH = 60°,所以∠ADH = 30°,所以AH = $\frac{1}{2}AD = 3$,所以DH = $\sqrt{AD^{2}-AH^{2}} = 3\sqrt{3}$,所以△ADF的面积 = $\frac{1}{2}AF\cdot DH=\frac{1}{2}\times6\times3\sqrt{3}=9\sqrt{3}$。
查看更多完整答案,请扫码查看


