《2025年5年中考3年模拟八年级数学下册人教版》

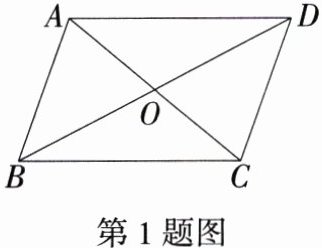
1.(2024河北邢台期末)如图，在□ABCD中，AD = 3，对角线AC与BD相交于点O，AC + BD = 12，则△BOC的周长为 ( )

A.8
B.9
C.12
D.15

答案： B：因为四边形 $ABCD$ 是平行四边形，所以 $AO = OC=\frac{1}{2}AC$，$BO = OD=\frac{1}{2}BD$，$BC = AD = 3$。又因为 $AC + BD = 12$，所以 $OC + BO = 6$，则 $C_{\triangle BOC}=OC + OB + BC = 6 + 3 = 9$，故选 B。

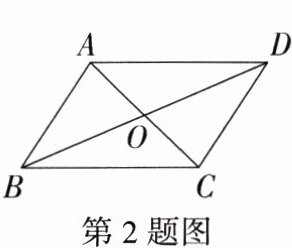
2.(2023广东广州华侨外国语学校期末)如图，在四边形ABCD中，对角线AC和BD相交于点O，下列条件不能判定四边形ABCD是平行四边形的是 ( )

A.AB//DC，AD//BC
B.AB = DC，AD = BC
C.AB//DC，AD = BC
D.OA = OC，OB = OD

答案： C：根据两组对边分别平行的四边形是平行四边形可知选项 A 中的条件可以判定四边形 $ABCD$ 是平行四边形；根据两组对边分别相等的四边形是平行四边形可知选项 B 中的条件可以判定四边形 $ABCD$ 是平行四边形；根据一组对边平行，另一组对边相等无法判定四边形 $ABCD$ 是平行四边形，故选项 C 中的条件不能判定四边形 $ABCD$ 是平行四边形；根据对角线互相平分的四边形是平行四边形可知选项 D 中的条件可以判定四边形 $ABCD$ 是平行四边形。故选 C。

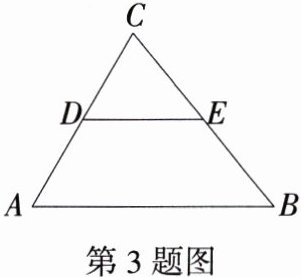
3.(2024河南郑州期末)如图，D、E分别为△ABC边AC、BC的中点，∠A = 60°，DE = 6，则下列结论错误的是 ( )

A.∠ADE = 120°
B.AB = 12
C.∠CDE = 60°
D.DC = 6

答案： D：因为 $D$、$E$ 分别为 $\triangle ABC$ 边 $AC$、$BC$ 的中点，所以 $DE$ 是 $\triangle ABC$ 的中位线，所以 $DE// AB$，且 $DE=\frac{1}{2}AB$，所以 $\angle CDE=\angle A$，$\angle ADE+\angle A = 180^{\circ}$，$AB = 2DE$。又因为 $\angle CDE = 60^{\circ}$，$\angle ADE = 120^{\circ}$，$AB = 12$，故选项 A、B、C 的结论正确，无法判断 D 选项结论的正误。故选 D。

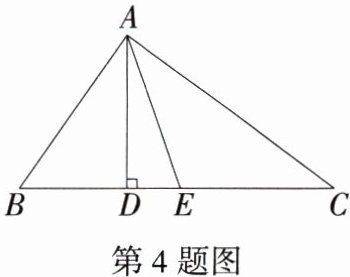
4.(2024湖北武汉期末)如图，在Rt△ABC中，∠BAC = 90°，AD⊥BC于点D，∠BAD = 35°，E是斜边BC的中点，则∠DAE的度数为 ( )

A.15°
B.20°
C.25°
D.30°

答案： B：因为 $AD\perp BC$，所以 $\angle ADB = 90^{\circ}$。因为 $\angle BAD = 35^{\circ}$，所以 $\angle B = 90^{\circ}-\angle BAD = 55^{\circ}$。因为 $\angle BAC = 90^{\circ}$，$E$ 是斜边 $BC$ 的中点，所以 $AE = BE=\frac{1}{2}BC$，所以 $\angle BAE=\angle B = 55^{\circ}$，所以 $\angle DAE=\angle BAE-\angle BAD = 20^{\circ}$，故选 B。

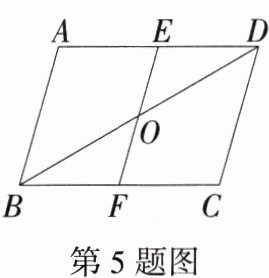
5.(2024四川眉山中考)如图，在□ABCD中，点O是BD的中点，EF过点O，下列结论：①AB//DC；②EO = ED；③∠A = ∠C；④S_{四边形ABOE}=S_{四边形CDOF}.其中正确结论的个数为 ( )

A.1
B.2
C.3
D.4

答案： C：因为四边形 $ABCD$ 是平行四边形，所以 $AB// DC$，$AD// BC$，$\angle A=\angle C$，故①③正确。因为 $AD// BC$，所以 $\angle ODE=\angle OBF$。因为点 $O$ 是 $BD$ 的中点，所以 $OD = OB$。又因为 $\angle DOE=\angle BOF$，所以 $\triangle ODE\cong\triangle OBF(ASA)$，所以 $S_{\triangle ODE}=S_{\triangle OBF}$，$EO = FO$。根据已知条件不能推出 $EO = ED$，故②不正确。因为 $S_{\triangle ABD}=S_{\triangle CDB}=\frac{1}{2}S_{\square ABCD}$，$S_{\triangle ODE}=S_{\triangle OBF}$，所以 $S_{\triangle ABD}-S_{\triangle ODE}=S_{\triangle CDB}-S_{\triangle OBF}$，所以 $S_{四边形ABOE}=S_{四边形CDOF}$，故④正确。综上所述，正确结论的个数为 3，故选 C。

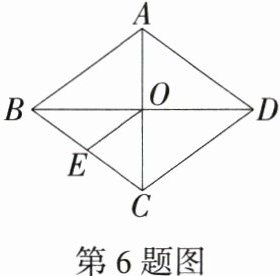
6.(2023四川乐山中考)如图，菱形ABCD的对角线AC与BD相交于点O，E为边BC的中点，连接OE.若AC = 6，BD = 8，则OE = ( )

A.2
B.$\frac{5}{2}$
C.3
D.4

答案： B：因为四边形 $ABCD$ 是菱形，所以 $OC=\frac{1}{2}AC$，$OB=\frac{1}{2}BD$，$AC\perp BD$。因为 $AC = 6$，$BD = 8$，所以 $OC = 3$，$OB = 4$，所以 $BC=\sqrt{OB^{2}+OC^{2}} = 5$。因为 $E$ 为边 $BC$ 的中点，所以 $OE=\frac{1}{2}BC=\frac{5}{2}$。故选 B。

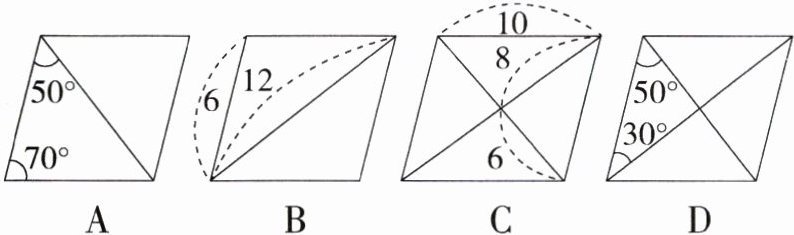
7.(2023浙江宁波期末)根据平行四边形中所标注的角的度数和线段的长度，下列一定能判定其为菱形的是 ( )

答案： C：A. 由题图中标注的角的度数可知平行四边形的邻边不相等，不能判定为菱形，故选项 A 不符合题意；B. 由题图中标注的线段的长度不能得到平行四边形的邻边相等，不能判定为菱形，故选项 B 不符合题意；C. 因为 $6^{2}+8^{2}=10^{2}$，所以对角线互相垂直，所以题图中的平行四边形为菱形，故选项 C 符合题意；D. 由题图中标注的角的度数可知平行四边形的对角线不互相垂直，不能判定为菱形，故选项 D 不符合题意。故选 C。

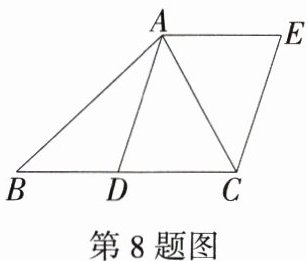
8.如图，AD是△ABC的中线，四边形ADCE是平行四边形，增加下列条件，能判定四边形ADCE是矩形的是 ( )

A.∠BAC = 90°
B.AE = CE
C.AB = AC
D.AB = AE

答案： C：A. 因为 $AD$ 是 $\triangle ABC$ 的中线，$\angle BAC = 90^{\circ}$，所以 $AD = BD = CD$。因为四边形 $ADCE$ 是平行四边形，所以四边形 $ADCE$ 为菱形，不符合题意；B. 因为四边形 $ADCE$ 是平行四边形，$AE = CE$，所以四边形 $ADCE$ 为菱形，不符合题意；C. 因为 $AD$ 是 $\triangle ABC$ 的中线，$AB = AC$，所以 $\angle ADC = 90^{\circ}$。因为四边形 $ADCE$ 是平行四边形，所以四边形 $ADCE$ 是矩形，符合题意；D. 因为四边形 $ADCE$ 是平行四边形，所以 $AE = CD$。因为 $AD$ 是 $\triangle ABC$ 的中线，所以 $BD = CD$。因为 $AB = AE$，所以 $BD = AB$，所以 $\angle BDA=\angle BAD$。根据三角形内角和等于 $180^{\circ}$，可得 $\angle BDA\lt90^{\circ}$，所以四边形 $ADCE$ 不是矩形，不符合题意。故选 C。

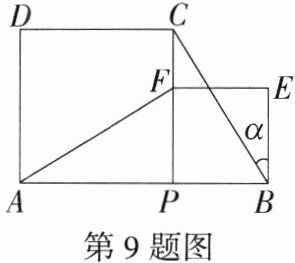
9.(2021江苏泰州中考)如图，P为AB上任意一点，分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF，设∠CBE = α，则∠AFP = ( )

A.2α
B.90° - α
C.45° + α
D.90° - $\frac{1}{2}$α

答案： B：因为四边形 $PBEF$ 为正方形，所以 $\angle PBE = 90^{\circ}$，$PF = PB$。因为 $\angle CBE=\alpha$，所以 $\angle PBC = 90^{\circ}-\alpha$。因为四边形 $APCD$ 是正方形，所以 $\angle APF = 90^{\circ}=\angle CPB$，$AP = CP$。在 $\triangle APF$ 和 $\triangle CPB$ 中，$\begin{cases}AP = CP\\\angle APF=\angle CPB\\PF = PB\end{cases}$，所以 $\triangle APF\cong\triangle CPB(SAS)$，所以 $\angle AFP=\angle PBC = 90^{\circ}-\alpha$。故选 B。