第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024湖北武汉期末)某登山队测得的气温(单位:℃)与海拔(单位:km)的对应关系如下表:
|海拔/km|…|1|1.5|2|2.5|3|…|
|气温/℃|…|-1|-4|-7|-10|-13|…|
若在某处测得的气温为-19℃,则该处的海拔为 ( )
A.4 km
B.4.5 km
C.5 km
D.-2 km
|海拔/km|…|1|1.5|2|2.5|3|…|
|气温/℃|…|-1|-4|-7|-10|-13|…|
若在某处测得的气温为-19℃,则该处的海拔为 ( )
A.4 km
B.4.5 km
C.5 km
D.-2 km
答案:
A:设登山队测得的气温为$y\ ^{\circ}C$,海拔为$x\ km$,由题表可知,$y = -1+\frac{-4 - (-1)}{1.5 - 1}(x - 1)=5 - 6x$。当$y = -19$时,$-19 = 5 - 6x$,解得$x = 4$。故选A。
2.(跨物理·弹簧变形)弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)的关系如下表(在弹性限度内),那么弹簧的长度y(cm)与所挂重物的质量x(kg)之间的关系式为 ( )
|x(kg)|0|1|2|3|4|5|6|
|y(cm)|12|12.5|13|13.5|14|14.5|15|
A.y = 0.5x + 12
B.y = x + 10.5
C.y = 0.5x + 10
D.y = x + 12
|x(kg)|0|1|2|3|4|5|6|
|y(cm)|12|12.5|13|13.5|14|14.5|15|
A.y = 0.5x + 12
B.y = x + 10.5
C.y = 0.5x + 10
D.y = x + 12
答案:
A:由题表数据可得出弹簧的长度$y(cm)$与所挂重物的质量$x(kg)$之间的关系式为$y = 0.5x + 12$。
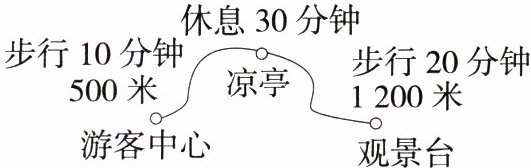
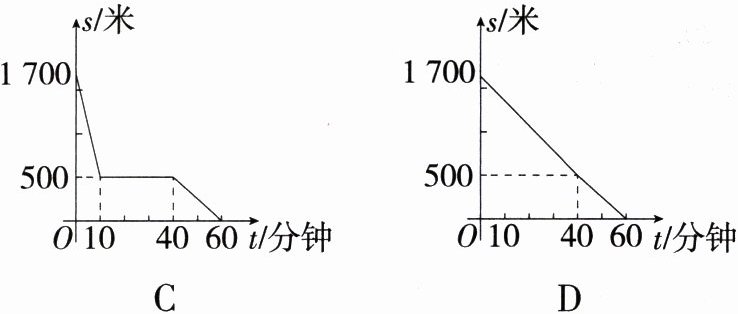
3.笑笑一家到达植物园后从游客中心出发去观景台游玩的行程如图所示,他们离游客中心的路程为s(米),所经过的时间为t(分钟).下列选项中的图象能近似刻画s与t之间的关系的是 ( )




答案:
A:由题意可知,笑笑一家在植物园从游客中心出发去观景台,即随着$t$的增大,$s$也在增大,所以选项C、D错误;他们在凉亭休息30分钟,所以A选项正确,B选项错误。故选A。
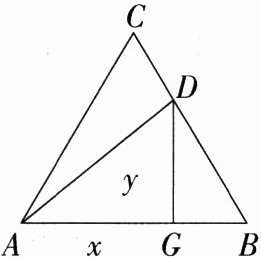
4.如图,等边△ABC的边长为1,点D从点A出发,沿A→C→B的路径运动,过D作AB边的垂线,交AB于G,连接AD,设线段AG的长度为x,Rt△AGD的面积为y,则y与x的函数表达式为______________.

答案:
答案:$y=\begin{cases}\frac{\sqrt{3}}{2}x^{2}(0 < x\leqslant\frac{1}{2})\\-\frac{\sqrt{3}}{2}x^{2}+\frac{\sqrt{3}}{2}x(\frac{1}{2} < x < 1)\end{cases}$
解析:当$0 < x\leqslant\frac{1}{2}$时,$y=\frac{1}{2}AG\cdot DG=\frac{\sqrt{3}}{2}x^{2}$;当$\frac{1}{2} < x < 1$时,$BG = 1 - x$,$DG=\sqrt{3}(1 - x)$,所以$y=\frac{1}{2}AG\cdot DG=\frac{1}{2}\cdot x\cdot\sqrt{3}(1 - x)=-\frac{\sqrt{3}}{2}x^{2}+\frac{\sqrt{3}}{2}x$,所以$y=\begin{cases}\frac{\sqrt{3}}{2}x^{2}(0 < x\leqslant\frac{1}{2})\\-\frac{\sqrt{3}}{2}x^{2}+\frac{\sqrt{3}}{2}x(\frac{1}{2} < x < 1)\end{cases}$。
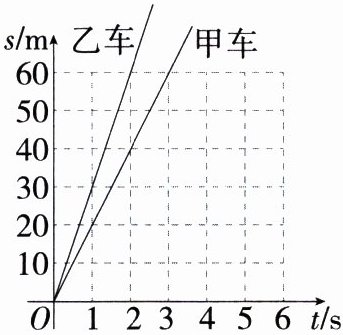
5.已知,甲、乙两车同时同地同向行驶,甲、乙两车距起点的距离s(m)与行驶时间t(s)之间的变化关系如图所示.
(1)若甲、乙两车之间的距离为y(m),请根据图象信息补全表格.
|行驶时间t/s|1|2|3|4|…|
|甲、乙两车之间的距离y/m| |30|40|…|
(2)请写出甲、乙两车之间的距离y(m)关于行驶时间t(s)的解析式.
(1)若甲、乙两车之间的距离为y(m),请根据图象信息补全表格.
|行驶时间t/s|1|2|3|4|…|
|甲、乙两车之间的距离y/m| |30|40|…|
(2)请写出甲、乙两车之间的距离y(m)关于行驶时间t(s)的解析式.

答案:
解析: (1)补全表格如下表所示: (2)根据题图可得,乙车的行驶速度为$60\div2 = 30(m/s)$,甲车的行驶速度为$40\div2 = 20(m/s)$,时间每增加1 s,甲、乙两车之间的距离增加$30 - 20 = 10(m)$,所以甲、乙两车之间的距离$y(m)$关于行驶时间$t(s)$的解析式为$y = 10t$。
(2)根据题图可得,乙车的行驶速度为$60\div2 = 30(m/s)$,甲车的行驶速度为$40\div2 = 20(m/s)$,时间每增加1 s,甲、乙两车之间的距离增加$30 - 20 = 10(m)$,所以甲、乙两车之间的距离$y(m)$关于行驶时间$t(s)$的解析式为$y = 10t$。
解析: (1)补全表格如下表所示:
 (2)根据题图可得,乙车的行驶速度为$60\div2 = 30(m/s)$,甲车的行驶速度为$40\div2 = 20(m/s)$,时间每增加1 s,甲、乙两车之间的距离增加$30 - 20 = 10(m)$,所以甲、乙两车之间的距离$y(m)$关于行驶时间$t(s)$的解析式为$y = 10t$。
(2)根据题图可得,乙车的行驶速度为$60\div2 = 30(m/s)$,甲车的行驶速度为$40\div2 = 20(m/s)$,时间每增加1 s,甲、乙两车之间的距离增加$30 - 20 = 10(m)$,所以甲、乙两车之间的距离$y(m)$关于行驶时间$t(s)$的解析式为$y = 10t$。 查看更多完整答案,请扫码查看


