第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
18. [易错题] (2023黑龙江齐齐哈尔中考, 13, ★☆☆) 在函数y = $\frac{1}{\sqrt{x - 1}}$ + $\frac{1}{x - 2}$中, 自变量x的取值范围是____________.
答案:
答案 x>1且x≠2
解析 由题意得x - 1>0,且x - 2≠0,
解得x>1且x≠2.
易错点 在求函数自变量的取值范围时,当二次根式在分母处时,容易因忽视分母不等于0的情况而导致错误.
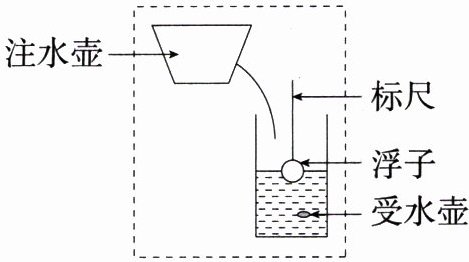
19. (2024山东烟台一中月考, 18, ★☆☆) 如图, 小珍依据漏刻的基本原理做了一个底面积为2 cm², 容积为20 cm³的圆柱形漏刻(浮子体积忽略不计), 观测并记录了水位h (cm) 与时间t (min) 之间的数据如下:
|t (min)|0|1|2|3|4|5|…|
|h (cm)|1|1.25|1.5|1.75|2|2.25|…|
(1) 请写出水位h (cm) 与时间t (min) 之间的函数解析式, 并确定自变量的取值范围.
(2) 当h = 5时, 求对应的时间t, 并说明它表示的实际意义.
|t (min)|0|1|2|3|4|5|…|
|h (cm)|1|1.25|1.5|1.75|2|2.25|…|
(1) 请写出水位h (cm) 与时间t (min) 之间的函数解析式, 并确定自变量的取值范围.
(2) 当h = 5时, 求对应的时间t, 并说明它表示的实际意义.

答案:
解析 (1)由题表中的数据可得,初始时,水位高度为1 cm,时间每增加1 min,水位的高度增加0.25 cm,故水位h(cm)与时间t(min)之间的函数解析式为h = 0.25t + 1,
∵ 漏刻的容积为20 cm³,底面积为2 cm²,
∴ 漏刻的高度为20÷2 = 10(cm), 当h = 10时,10 = 0.25t + 1, 解得t = 36,
∴ 自变量的取值范围为0≤t≤36. (2)当h = 5时,5 = 0.25t + 1,解得t = 16, 实际意义:当漏刻的水位高度为5 cm时,计时时长为16 min.
∵ 漏刻的容积为20 cm³,底面积为2 cm²,
∴ 漏刻的高度为20÷2 = 10(cm), 当h = 10时,10 = 0.25t + 1, 解得t = 36,
∴ 自变量的取值范围为0≤t≤36. (2)当h = 5时,5 = 0.25t + 1,解得t = 16, 实际意义:当漏刻的水位高度为5 cm时,计时时长为16 min.
20. (2022浙江宁波外国语学校月考改编, 18, ★☆☆) 将长为40 cm, 宽为15 cm的长方形白纸按如图所示的方法黏合起来, 黏合部分的宽为5 cm.
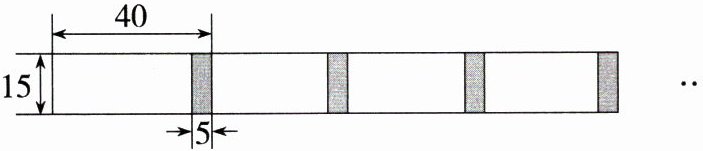
(1) 根据图形, 将表格补充完整:
|白纸张数|1|2|3|4|5|…|
|纸条长度(cm)|40| |110|145| |…|
(2) 设x张白纸黏合后的总长度为y cm, 求y与x之间的关系式(不用写x的取值范围).
(3) 你认为将若干张白纸黏合起来的总长度可能为2 024 cm吗? 为什么?

(1) 根据图形, 将表格补充完整:
|白纸张数|1|2|3|4|5|…|
|纸条长度(cm)|40| |110|145| |…|
(2) 设x张白纸黏合后的总长度为y cm, 求y与x之间的关系式(不用写x的取值范围).
(3) 你认为将若干张白纸黏合起来的总长度可能为2 024 cm吗? 为什么?
答案:
解析 (1)补充表格如下: (2)由(1)中表格可知,每增加1张白纸,总长度增加35 cm,所以y与x之间的关系式为y = 40 + 35(x - 1) = 35x + 5.
(3)不可能. 理由如下:
当y = 2024时,2024 = 35x + 5,解得x = $\frac{2019}{35}$,
因为x应为整数,所以将若干张白纸黏合起来的总长度不可能为2024 cm.
(2)由(1)中表格可知,每增加1张白纸,总长度增加35 cm,所以y与x之间的关系式为y = 40 + 35(x - 1) = 35x + 5.
(3)不可能. 理由如下:
当y = 2024时,2024 = 35x + 5,解得x = $\frac{2019}{35}$,
因为x应为整数,所以将若干张白纸黏合起来的总长度不可能为2024 cm.
解析 (1)补充表格如下:
 (2)由(1)中表格可知,每增加1张白纸,总长度增加35 cm,所以y与x之间的关系式为y = 40 + 35(x - 1) = 35x + 5.
(3)不可能. 理由如下:
当y = 2024时,2024 = 35x + 5,解得x = $\frac{2019}{35}$,
因为x应为整数,所以将若干张白纸黏合起来的总长度不可能为2024 cm.
(2)由(1)中表格可知,每增加1张白纸,总长度增加35 cm,所以y与x之间的关系式为y = 40 + 35(x - 1) = 35x + 5.
(3)不可能. 理由如下:
当y = 2024时,2024 = 35x + 5,解得x = $\frac{2019}{35}$,
因为x应为整数,所以将若干张白纸黏合起来的总长度不可能为2024 cm. 21. [推理能力] 将一张长方形的纸对折, 如图①, 可得到一条折痕, 继续对折, 对折时每条折痕与上次的折痕保持平行, 如图②, 连续对折3次后, 可以得到7条折痕, 如图③.

回答下列问题:
(1) 对折4次可以得到_______条折痕.
(2) 写出折痕的条数y与对折次数x之间的函数关系式.
(3) 求出对折10次后的折痕条数.

回答下列问题:
(1) 对折4次可以得到_______条折痕.
(2) 写出折痕的条数y与对折次数x之间的函数关系式.
(3) 求出对折10次后的折痕条数.
答案:
解析 (1)第1次对折有2 - 1 = 1条折痕,第2次对折有2² - 1 = 3条折痕,第3次对折有2³ - 1 = 7条折痕,第4次对折有2⁴ - 1 = 15条折痕,所以对折4次可以得到15条折痕.
(2)根据(1)可得到y = 2ˣ - 1(x为正整数).
(3)当x = 10时,y = 2¹⁰ - 1 = 1023,
所以对折10次后的折痕条数为1023.
查看更多完整答案,请扫码查看


