第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
15.应用意识 探究:如图1,在平行四边形ABCD中,AC,BD交于点O,过点O的直线交AD于点E,交BC于点F.
(1)求证:四边形AEFB与四边形DEFC的周长相等.
(2)直线EF是否将平行四边形ABCD的面积分成二等份? 试说明理由.
应用:
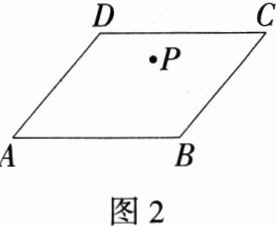
(3)张大爷家有一块平行四边形菜园,园中有一口水井P,如图2,张大爷计划把菜园平均分成两块,分别种植西红柿和茄子,且使两块地共用这口水井,请你帮助张大爷把地分开.
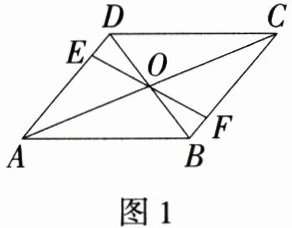
(1)求证:四边形AEFB与四边形DEFC的周长相等.
(2)直线EF是否将平行四边形ABCD的面积分成二等份? 试说明理由.
应用:
(3)张大爷家有一块平行四边形菜园,园中有一口水井P,如图2,张大爷计划把菜园平均分成两块,分别种植西红柿和茄子,且使两块地共用这口水井,请你帮助张大爷把地分开.


答案:
解析
(1)证明:
∵ 四边形ABCD是平行四边形,
∴ AB = CD,OA = OC,AD//BC,
∴ ∠OAE = ∠OCF, 在△OAE和△OCF中,$\begin{cases}\angle OAE=\angle OCF \\ OA = OC \\ \angle AOE=\angle COF\end{cases}$,
∴ △OAE≌△OCF(ASA),
∴ AE = CF, 同理可证△ODE≌△OBF,
∴ DE = BF,
∴ AB + AE + EF + BF = CD + CF + EF + DE,
∴ 四边形AEFB与四边形DEFC的周长相等.
(2)直线EF是将平行四边形ABCD的面积分成二等份. 理由如下:
∵ 四边形ABCD是平行四边形,
∴ AB = CD,OA = OC,OB = OD, 在△AOB和△COD中,$\begin{cases}AB = CD \\ OA = OC \\ OB = OD\end{cases}$,
∴ △AOB≌△COD(SSS),
∴ $S_{\triangle AOB}=S_{\triangle COD}$, 由
(1)得△OAE≌△OCF,△ODE≌△OBF,
∴ $S_{\triangle OAE}=S_{\triangle OCF}$,$S_{\triangle ODE}=S_{\triangle OBF}$,
∴ $S_{\triangle AOB}+S_{\triangle OAE}+S_{\triangle OBF}=S_{\triangle COD}+S_{\triangle OCF}+S_{\triangle ODE}$,
∴ 直线EF将平行四边形ABCD的面积分成二等份.
(3)连接AC,BD交于点O,作直线OP,则直线OP两侧的四边形面积相等,如图所示.
解析
(1)证明:
∵ 四边形ABCD是平行四边形,
∴ AB = CD,OA = OC,AD//BC,
∴ ∠OAE = ∠OCF, 在△OAE和△OCF中,$\begin{cases}\angle OAE=\angle OCF \\ OA = OC \\ \angle AOE=\angle COF\end{cases}$,
∴ △OAE≌△OCF(ASA),
∴ AE = CF, 同理可证△ODE≌△OBF,
∴ DE = BF,
∴ AB + AE + EF + BF = CD + CF + EF + DE,
∴ 四边形AEFB与四边形DEFC的周长相等.
(2)直线EF是将平行四边形ABCD的面积分成二等份. 理由如下:
∵ 四边形ABCD是平行四边形,
∴ AB = CD,OA = OC,OB = OD, 在△AOB和△COD中,$\begin{cases}AB = CD \\ OA = OC \\ OB = OD\end{cases}$,
∴ △AOB≌△COD(SSS),
∴ $S_{\triangle AOB}=S_{\triangle COD}$, 由
(1)得△OAE≌△OCF,△ODE≌△OBF,
∴ $S_{\triangle OAE}=S_{\triangle OCF}$,$S_{\triangle ODE}=S_{\triangle OBF}$,
∴ $S_{\triangle AOB}+S_{\triangle OAE}+S_{\triangle OBF}=S_{\triangle COD}+S_{\triangle OCF}+S_{\triangle ODE}$,
∴ 直线EF将平行四边形ABCD的面积分成二等份.
(3)连接AC,BD交于点O,作直线OP,则直线OP两侧的四边形面积相等,如图所示.

16.推理能力 如图1,平行四边形ABCD的对角线AC、BD相交于点O,直线EF过点O与AD、BC相交于点E、F.
(1)求证:OE=OF.
(2)若直线EF分别与DC、BA的延长线相交于F、E,如图2,则(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
(3)若平行四边形ABCD的面积为20,BC=10,CD=6,直线EF在绕点O旋转的过程中,线段EF何时最短? 并求出EF的最小值.
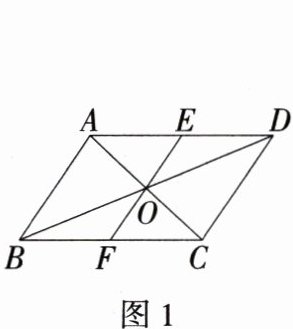

(1)求证:OE=OF.
(2)若直线EF分别与DC、BA的延长线相交于F、E,如图2,则(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
(3)若平行四边形ABCD的面积为20,BC=10,CD=6,直线EF在绕点O旋转的过程中,线段EF何时最短? 并求出EF的最小值.


答案:
解析
(1)证明:
∵ 四边形ABCD是平行四边形,
∴ OA = OC,AD//BC,
∴ ∠OAE = ∠OCF, 在△AOE和△COF中,$\begin{cases}\angle OAE=\angle OCF \\ OA = OC \\ \angle AOE=\angle COF\end{cases}$,
∴ △AOE≌△COF,
∴ OE = OF.
(2)成立. 证明:
∵ 四边形ABCD是平行四边形,
∴ OA = OC,AB//CD,
∴ ∠E = ∠F, 在△OAE和△OCF中,$\begin{cases}\angle E=\angle F \\ \angle AOE=\angle COF \\ OA = OC\end{cases}$,
∴ △AOE≌△COF(AAS),
∴ OE = OF.
(3)①直线EF在绕点O旋转的过程中,若直线EF与AD,BC相交,则当EF⊥BC时,EF最短,
∵ 平行四边形ABCD的面积为20,BC = 10,
∴ $S_{平行四边形ABCD}=BC\cdot EF = 10×EF = 20$,
∴ EF = 2,
∴ 直线EF在绕点O旋转的过程中,EF⊥BC时,EF最短,EF的最小值为2. ②直线EF在绕点O旋转的过程中,若直线EF与DC、BA的延长相交相交,则当EF⊥AB时,EF最短, 同①的方法,得出EF的最小值为$\frac{20}{6}=\frac{10}{3}$. 故直线EF绕绕点O旋转的过程中,EF⊥BC时,EF最短,EF的最小值为2.
(1)证明:
∵ 四边形ABCD是平行四边形,
∴ OA = OC,AD//BC,
∴ ∠OAE = ∠OCF, 在△AOE和△COF中,$\begin{cases}\angle OAE=\angle OCF \\ OA = OC \\ \angle AOE=\angle COF\end{cases}$,
∴ △AOE≌△COF,
∴ OE = OF.
(2)成立. 证明:
∵ 四边形ABCD是平行四边形,
∴ OA = OC,AB//CD,
∴ ∠E = ∠F, 在△OAE和△OCF中,$\begin{cases}\angle E=\angle F \\ \angle AOE=\angle COF \\ OA = OC\end{cases}$,
∴ △AOE≌△COF(AAS),
∴ OE = OF.
(3)①直线EF在绕点O旋转的过程中,若直线EF与AD,BC相交,则当EF⊥BC时,EF最短,
∵ 平行四边形ABCD的面积为20,BC = 10,
∴ $S_{平行四边形ABCD}=BC\cdot EF = 10×EF = 20$,
∴ EF = 2,
∴ 直线EF在绕点O旋转的过程中,EF⊥BC时,EF最短,EF的最小值为2. ②直线EF在绕点O旋转的过程中,若直线EF与DC、BA的延长相交相交,则当EF⊥AB时,EF最短, 同①的方法,得出EF的最小值为$\frac{20}{6}=\frac{10}{3}$. 故直线EF绕绕点O旋转的过程中,EF⊥BC时,EF最短,EF的最小值为2.
查看更多完整答案,请扫码查看


