《2025年5年中考3年模拟八年级数学下册人教版》

10.新考向·尺规作图(2023山东日照一模)如图，在矩形ABCD中，AB ＜ BC，连接AC，分别以点A，C为圆心，大于$\frac{1}{2}$AC长为半径画弧，两弧交于点M，N，直线MN分别交AD，BC，AC于点E，F，O，连接CE，AF.下列结论：①四边形AECF是菱形；②∠AFB = 2∠ACB；③AC·EF = CF·CD；④若AF平分∠BAC，则CF = $\sqrt{3}$AB.其中正确结论的个数是 ( )


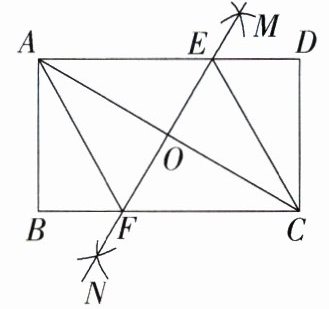
A.4
B.3
C.2
D.1

答案： C：根据作图知 $EF$ 垂直平分 $AC$，所以 $AO = CO$。因为 $AD// BC$，所以 $\angle EAO=\angle FCO$。在 $\triangle AOE$ 和 $\triangle COF$ 中，$\begin{cases}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF = 90^{\circ}\end{cases}$，所以 $\triangle AOE\cong\triangle COF(ASA)$，所以 $OE = OF$。因为 $OA = OC$，$AC\perp EF$，所以四边形 $AECF$ 是菱形，故结论①正确；因为 $EF$ 垂直平分 $AC$，所以 $AF = CF$，所以 $\angle FAC=\angle FCA$。因为 $\angle AFB=\angle FAO+\angle ACB$，所以 $\angle AFB = 2\angle ACB$，故结论②正确；$S_{四边形AECF}=CF\cdot CD=\frac{1}{2}AC\cdot EF$，故结论③不正确；因为四边形 $AECF$ 为菱形，所以 $\angle FAC=\angle EAC$，因为 $AF$ 平分 $\angle BAC$，所以 $\angle BAF=\angle FAC=\angle CAD=\frac{1}{3}\times90^{\circ}=30^{\circ}$，所以 $AF = 2BF$，所以 $AB=\sqrt{3}BF$。因为 $CF = AF$，所以 $CF = 2BF=\frac{2\sqrt{3}}{3}AB$，故结论④不正确。故选 C。

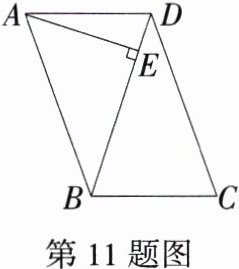
11.(2024湖南衡阳期末)如图，在□ABCD中，BA = BD，AE⊥BD，若∠C = 70°，则∠DAE的度数为________.

答案： 答案：$20^{\circ}$ 解析：因为四边形 $ABCD$ 是平行四边形，所以 $CD = AB$，$AD// BC$。因为 $BD = AB$，所以 $CD = BD$，所以 $\angle DBC=\angle C = 70^{\circ}$。因为 $AD// BC$，所以 $\angle ADE=\angle DBC = 70^{\circ}$。因为 $AE\perp BD$，所以 $\angle DAE = 90^{\circ}-70^{\circ}=20^{\circ}$。

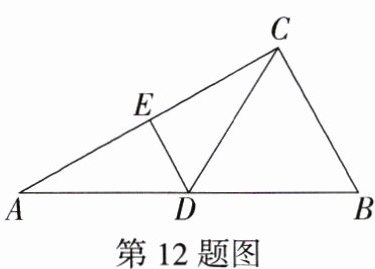
12.(2023湖南长沙二模)如图，在Rt△ABC中，∠ACB = 90°，点D是斜边AB的中点，DE平分∠ADC，BC = 4，则DE的长是________.

答案： 答案：$2$ 解析：因为 $\angle ACB = 90^{\circ}$，点 $D$ 是斜边 $AB$ 的中点，所以 $AD = CD=\frac{1}{2}AB$。因为 $DE$ 平分 $\angle ADC$，所以 $AE = EC$，所以 $ED$ 是 $\triangle ABC$ 的中位线，所以 $DE=\frac{1}{2}BC = 2$。

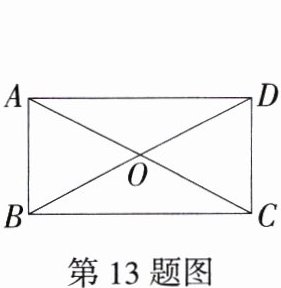
13.(2024重庆育才学校期末)如图，矩形ABCD中，AB = 4，对角线AC，BD交于点O，若∠AOB = 60°，则矩形ABCD的面积为________.

答案： 答案：$16\sqrt{3}$ 解析：因为四边形 $ABCD$ 是矩形，所以 $AC = 2AO$，$BD = 2BO$，$AC = BD$，$\angle ABC = 90^{\circ}$，所以 $AO = OB$。因为 $\angle AOB = 60^{\circ}$，所以 $\triangle AOB$ 是等边三角形，所以 $OA = AB = 4$，所以 $AC = 2AO = 8$，所以 $BC=\sqrt{AC^{2}-AB^{2}}=\sqrt{64 - 16}=4\sqrt{3}$，所以矩形 $ABCD$ 的面积 $=AB\cdot BC = 4\times4\sqrt{3}=16\sqrt{3}$。

14.如图，在菱形ABCD中，对角线AC、BD相交于点O，点E、F分别是AB、AO的中点，连接EF.若AF = 1，AE = $\sqrt{3}$，则菱形ABCD的面积为________.

答案： 答案：$8\sqrt{2}$ 解析：因为点 $E$、$F$ 分别是 $AB$、$AO$ 的中点，所以 $AB = 2AE = 2\sqrt{3}$，$AO = 2AF = 2$。因为四边形 $ABCD$ 是菱形，所以 $AO = CO$，$BO = DO$，$AC\perp BD$，所以 $BO=\sqrt{AB^{2}-AO^{2}}=\sqrt{12 - 4}=2\sqrt{2}$，所以 $BD = 2BO = 4\sqrt{2}$。又因为 $AC = 2AO = 4$，所以菱形 $ABCD$ 的面积 $=\frac{AC\cdot BD}{2}=\frac{4\times4\sqrt{2}}{2}=8\sqrt{2}$。

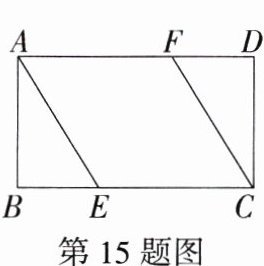
15.(2021北京中考)如图，在矩形ABCD中，点E，F分别在BC，AD上，AF = EC，只需添加一个条件即可证明四边形AECF是菱形，这个条件可以是________(写出一个即可).

答案： 答案：$AE = AF$（答案不唯一） 解析：答案不唯一，如添加条件 $AE = AF$。理由如下：在矩形 $ABCD$ 中，$AD// BC$，即 $AF// CE$，因为 $AF = EC$，所以四边形 $AECF$ 是平行四边形。因为 $AE = AF$，所以四边形 $AECF$ 是菱形。

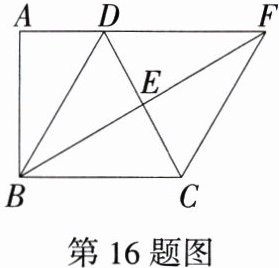
16.(2024江苏无锡二模)如图，在四边形ABCD中，AD//BC，∠A = 90°，BD = BC，点E为CD的中点，射线BE交AD的延长线于点F，连接CF.若AD = 1，CF = 2，则BF的长为________.

答案： 答案：$2\sqrt{3}$ 解析：因为 $AD// BC$，所以 $\angle FDE=\angle BCE$。因为点 $E$ 为 $CD$ 的中点，所以 $DE = EC$。在 $\triangle BCE$ 与 $\triangle FDE$ 中，$\begin{cases}\angle BCE=\angle FDE\\CE = DE\\\angle BEC=\angle FED\end{cases}$，所以 $\triangle BCE\cong\triangle FDE(ASA)$，所以 $BC = FD$。因为 $AD// BC$，所以四边形 $BCFD$ 为平行四边形。又因为 $BD = BC$，所以平行四边形 $BCFD$ 是菱形，所以 $BD = DF = CF = 2$，所以 $AF = AD + DF = 3$。因为 $\angle A = 90^{\circ}$，所以 $AB=\sqrt{BD^{2}-AD^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$，所以 $BF=\sqrt{AB^{2}+AF^{2}}=\sqrt{(\sqrt{3})^{2}+3^{2}}=2\sqrt{3}$。

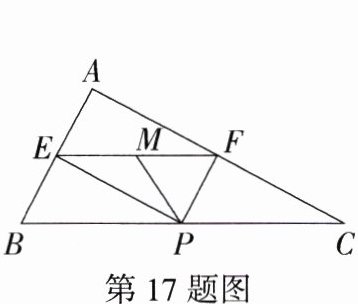
17.(2023广东珠海期中)如图，在△ABC中，∠BAC = 90°，AB = 12，AC = 16，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，则PM的最小值为________.

答案：
答案：$4.8$ 解析：连接 $AP$，如图所示。
因为 $\angle BAC = 90^{\circ}$，$AB = 12$，$AC = 16$，所以 $BC=\sqrt{12^{2}+16^{2}} = 20$。因为 $PE\perp AB$，$PF\perp AC$，所以四边形 $AFPE$ 是矩形，所以 $EF = AP$，$EF$ 与 $AP$ 互相平分。因为 $M$ 是 $EF$ 的中点，所以 $M$ 为 $AP$ 的中点，所以 $PM=\frac{1}{2}AP$。当 $AP\perp BC$ 时，$AP$ 的值最小，同样 $PM$ 的值也最小，此时 $AP=\frac{AB\cdot AC}{BC}=9.6$，所以 $PM=\frac{1}{2}AP = 4.8$，所以 $PM$ 的最小值为 $4.8$。

18.(2020山东枣庄中考)如图，E，F是正方形ABCD的对角线AC上的两点，AC = 8，AE = CF = 2，则四边形BEDF的周长是________.

答案：
答案：$8\sqrt{5}$ 解析：如图，连接 $BD$ 交 $AC$ 于点 $O$。
因为四边形 $ABCD$ 为正方形，$AC = 8$，所以 $BD\perp AC$，$OD = OB = OA = OC = 4$。因为 $AE = CF = 2$，所以 $OA - AE = OC - CF$，即 $OE = OF = 2$，所以四边形 $BEDF$ 为平行四边形。因为 $BD\perp EF$，所以四边形 $BEDF$ 为菱形，所以 $DE = DF = BE = BF$。由勾股定理得 $DE=\sqrt{OD^{2}+OE^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$，所以四边形 $BEDF$ 的周长 $=4DE = 4\times2\sqrt{5}=8\sqrt{5}$。

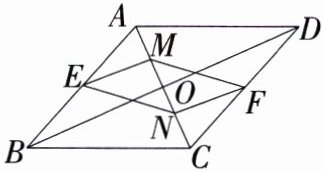
19.(2024河南驻马店期末)(8分)如图，在□ABCD中，点E，F分别是AB，CD的中点，点M，N在对角线AC上，且AM = CN.
(1)求证：四边形MENF是平行四边形.
(2)连接BD交AC于点O，若BD = 8，AM + CN = MN，求EM的长.

答案： 解析：（1）证明：因为四边形 $ABCD$ 是平行四边形，所以 $AB// CD$，$AB = CD$，所以 $\angle EAM=\angle FCN$。因为点 $E$，$F$ 分别是 $AB$，$CD$ 的中点，$AB = CD$，所以 $AE = CF$。因为 $AM = CN$，所以 $\triangle AEM\cong\triangle CFN(SAS)$，所以 $EM = FN$，$\angle AME=\angle CNF$，所以 $\angle EMN=\angle FNM$，所以 $EM// FN$。因为 $EM = FN$，所以四边形 $MENF$ 是平行四边形。（2）因为四边形 $ABCD$ 是平行四边形，所以 $OA = OC$，$OB = OD$。因为 $BD = 8$，所以 $OB = 4$。因为 $AM = CN$，$OA = OC$，所以 $OM = ON$。因为 $AM + CN = MN$，所以 $AM = OM = ON = CN$。因为点 $E$ 为 $AB$ 的中点，所以 $EM$ 为 $\triangle ABO$ 的中位线，所以 $EM=\frac{1}{2}OB = 2$。