《2025年5年中考3年模拟八年级数学下册人教版》

9.如图,菱形ABCD的边长为4,∠B = 120°,则菱形ABCD的面积为 ( )

A.6
B.4$\sqrt{3}$
C.8$\sqrt{3}$
D.12

答案： C 过D作DE⊥AB于E（图略），因为四边形ABCD是菱形，所以AD//BC，AD = AB = 4，因为∠B = 120°，所以∠A = 60°，所以∠ADE = 30°，所以AE = $\frac{1}{2}$AD = 2，所以DE = $\sqrt{AD^{2}-AE^{2}}=2\sqrt{3}$，所以菱形ABCD的面积是AB·DE = 4×2$\sqrt{3}$ = 8$\sqrt{3}$，故选C。

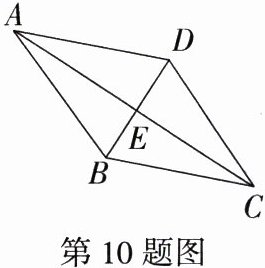
10.教材变式·P56例3 如图所示,四边形ABCD是边长为25 cm的菱形,其中对角线BD的长为14 cm,则对角线AC的长为__________cm,菱形ABCD的面积为__________cm².

答案： 答案：48；336 解析：因为四边形ABCD为菱形，BD = 14 cm，所以AC⊥BD，DE = $\frac{1}{2}$BD = $\frac{1}{2}$×14 = 7（cm），AC = 2AE，因为AD = 25 cm，所以AE = $\sqrt{AD^{2}-DE^{2}}=\sqrt{25^{2}-7^{2}} = 24$（cm），所以AC = 2AE = 2×24 = 48（cm），所以S菱形ABCD = $\frac{1}{2}$BD·AC = $\frac{1}{2}$×14×48 = 336（cm²）。

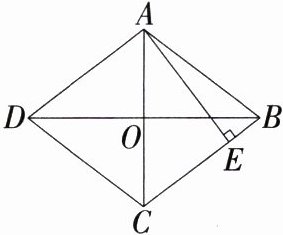
11.(2024黑龙江绥化中考,11,★★☆)如图,四边形ABCD是菱形,CD = 5,BD = 8,AE⊥BC于点E,则AE的长是 ( )

A.$\frac{24}{5}$
B.6
C.$\frac{48}{5}$
D.12

答案： A 因为四边形ABCD是菱形，CD = 5，BD = 8，所以BC = CD = 5，BO = DO = 4，OA = OC，AC⊥BD，所以∠BOC = 90°，在Rt△OBC中，由勾股定理得OC = $\sqrt{BC^{2}-BO^{2}}=\sqrt{5^{2}-4^{2}} = 3$，所以AC = 2OC = 6，因为菱形ABCD的面积 = AE·BC = $\frac{1}{2}$BD·AC = OB·AC，所以AE = $\frac{OB·AC}{BC}=\frac{4×6}{5}=\frac{24}{5}$，故选A。

12.(2023辽宁大连中考,13,★★☆)如图,在菱形ABCD中,AC、BD为菱形的对角线,∠DBC = 60°,BD = 10,点F为BC中点,则EF的长为__________.

答案： 答案：5 解析：因为四边形ABCD是菱形，所以BC = CD，AC⊥BD，因为∠DBC = 60°，所以△BDC是等边三角形，所以BC = BD = 10，因为∠BEC = 90°，点F为BC中点，所以EF = $\frac{1}{2}$BC = 5。

13.(2022黑龙江哈尔滨中考,20,★★☆)如图,菱形ABCD的对角线AC,BD相交于点O,点E在OB上,连接AE,点F为CD的中点,连接OF,若AE = BE,OE = 3,OA = 4,则线段OF的长为__________.

答案： 答案：2$\sqrt{5}$ 解析：因为四边形ABCD是菱形，所以AC⊥BD，CO = AO = 4，BC = CD，所以AE = $\sqrt{AO^{2}+EO^{2}}=\sqrt{16 + 9}=5$，所以BE = AE = 5，所以BO = 5 + 3 = 8，所以BC = $\sqrt{BO^{2}+CO^{2}}=\sqrt{64 + 16}=4\sqrt{5}$，因为点F为CD的中点，所以OF = $\frac{1}{2}$CD = $\frac{1}{2}$BC = 2$\sqrt{5}$。

14.(2024安徽池州月考,22,★★★)在菱形ABCD中,对角线AC,BD相交于点O,∠ABC = 45°,过点A作AM⊥BC于点M,交BD于点N.
(1)求∠CAM的度数.
(2)①求证:BN = 2OC.
②若AB = 4,求AN的长.

答案：
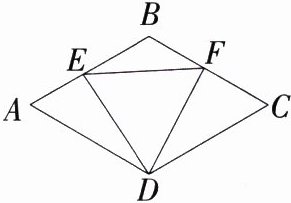
解析： （1）因为四边形ABCD是菱形，所以AB = BC，因为∠ABC = 45°，所以∠ACB = $\frac{1}{2}$(180° - ∠ABC)=67.5°，因为AM⊥BC，所以∠BMN = ∠AMC = 90°，所以∠CAM = 90° - ∠ACM = 90° - 67.5° = 22.5°。 （2）①证明：因为四边形ABCD是菱形，所以AC⊥BD，AC = 2OC，AB = BC = CD = DA，∠OBC = $\frac{1}{2}$∠ABC = 22.5°，由（1）知∠CAM = 22.5°，所以∠CAM = ∠OBC，因为∠BAM = 90° - 45° = 45° = ∠ABC，所以BM = AM，因为∠BMN = ∠AMC = 90°，所以△BMN≌△AMC（ASA），所以BN = AC = 2OC。 ②过点N作NH⊥AB于点H，如图所示。  因为四边形ABCD是菱形，所以BD平分∠ABC，又因为NH⊥AB，AM⊥BC，所以NM = NH，设NM = NH = x，因为∠ABC = 45°，所以△ABM与△AHN均为等腰直角三角形，所以AH = NH = x，AH² + HN² = AN²，AB² = AM² + BM² = 16，所以AN = $\sqrt{2}$x，BM = AM = 2$\sqrt{2}$，因为AM = AN + MN，所以x + $\sqrt{2}$x = 2$\sqrt{2}$，解得x = 4 - 2$\sqrt{2}$，所以AN = 4$\sqrt{2}-4$。

15.推理能力 半角模型 如图,在菱形ABCD中,E、F分别是AB、BC上一点,∠A = ∠EDF = 60°有下列结论:①AE = BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE = ∠BEF.其中正确的是 ( )

A.①②
B.②③④
C.①②③④
D.①②④

答案：
D 连接BD，如图。 因为四边形ABCD是菱形，所以AD = AB，∠ADB = $\frac{1}{2}$∠ADC，AB//CD，因为∠A = 60°，所以∠ADC = 120°，所以∠ADB = 60°，所以△ABD是等边三角形，所以AD = BD，同理可得∠DBF = 60°，所以∠A = ∠DBF，因为∠ADE + ∠BDE = 60°，∠BDE + ∠BDF = ∠EDF = 60°，所以∠ADE = ∠BDF，在△ADE和△BDF中，$\begin{cases}∠ADE = ∠BDF\\AD = BD\\∠A = ∠DBF\end{cases}$，所以△ADE≌△BDF（ASA），所以AE = BF，DE = DF，故①正确；因为∠EDF = 60°，所以△EDF是等边三角形，故②正确；由②得∠DEF = 60°，所以∠AED + ∠BEF = 120°，因为∠AED + ∠ADE = 180° - ∠A = 120°，所以∠ADE = ∠BEF，故④正确；同①可得△BDE≌△CDF，所以BE = CF，但BE不一定等于BF，故③错误。综上所述，结论正确的是①②④，故选D。