第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
15.已知$x = \frac{\sqrt{5}+1}{2}$,$y = \frac{\sqrt{5}-1}{2}$,则代数式$x^{2}+3xy + y^{2}$的值为________.
答案:
答案 6
解析 $\because x=\frac{\sqrt{5}+1}{2}$,$y=\frac{\sqrt{5}-1}{2}$,$\therefore x + y=\frac{\sqrt{5}+1}{2}+\frac{\sqrt{5}-1}{2}=\sqrt{5}$,$xy=\frac{\sqrt{5}+1}{2}\times\frac{\sqrt{5}-1}{2}=1$,$\therefore x^{2}+3xy + y^{2}=x^{2}+2xy + y^{2}+xy=(x + y)^{2}+xy=(\sqrt{5})^{2}+1=6$。
16.如图,一只蚂蚁从点$A$沿数轴向右爬行2个单位长度到达点$B$的位置,点$A$表示的数为$-\sqrt{2}$,设点$B$所表示的数为$m$,则$(m - 1)(m - 3)$的值是________.
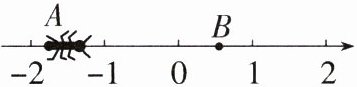
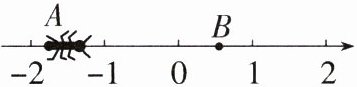
答案:
答案 1
解析 由题意得 $m=2-\sqrt{2}$,$\therefore(m - 1)(m - 3)=(2-\sqrt{2}-1)(2-\sqrt{2}-3)=(1-\sqrt{2})\times(-\sqrt{2}-1)=(-\sqrt{2})^{2}-1^{2}=2 - 1=1$。
17.(2024河南周口月考)已知$a$、$b$满足等式$b = \sqrt{2a - 6}+\sqrt{9 - 3a}-9$,则$\sqrt{12a}-\sqrt{b^{2}}+\sqrt[3]{ab}$的值为________.
答案:
答案 -6
解析 依题意得 $2a - 6\geq0$,$9 - 3a\geq0$,解得 $a = 3$,$\therefore b=0 + 0 - 9=-9$,$\therefore$原式 $=\sqrt{36}-\sqrt{81}+\sqrt[3]{-27}=6 - 9 - 3=-6$。
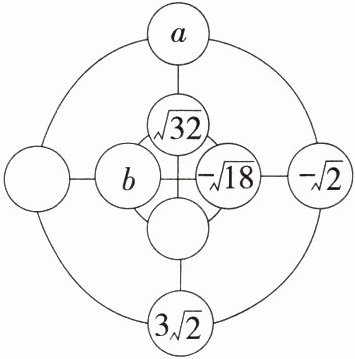
18.(情境题·数学文化)我国南宋数学家杨辉在《续古摘奇算法》中的攒九图中提出“幻圆”的概念.如图所示的是一个简单的二阶幻圆模型,若内、外两个圆周上四个数之和以及外圆两直径上的四个数之和都相等,则$a - b=$________.

答案:
答案 $-6\sqrt{2}$
解析 设外圆空白处的数为 $x$,内圆空白处的数为 $y$,根据题意得 $a + x+3\sqrt{2}+(-\sqrt{2})=\sqrt{32}+b + y+(-\sqrt{18})$,$a+\sqrt{32}+y+3\sqrt{2}=x + b+(-\sqrt{18})+(-\sqrt{2})$,整理得 $\begin{cases}a - b+x - y=4\sqrt{2}-3\sqrt{2}-3\sqrt{2}+\sqrt{2}=-\sqrt{2}①\\a - b+y - x=-3\sqrt{2}-\sqrt{2}-4\sqrt{2}-3\sqrt{2}=-11\sqrt{2}②\end{cases}$,$① + ②$得 $2(a - b)=-12\sqrt{2}$,则 $a - b=-6\sqrt{2}$。
19.(6分)计算或化简:
(1)$3\sqrt{1.25}\div\frac{3}{4}\sqrt{2\frac{1}{2}}\times2\sqrt{18}$.
(2)$\frac{3}{5}\sqrt{xy^{2}}\div(-\frac{4}{15}\sqrt{\frac{y}{x}})\cdot(-\frac{5}{6}\sqrt{x^{3}y})$.
(1)$3\sqrt{1.25}\div\frac{3}{4}\sqrt{2\frac{1}{2}}\times2\sqrt{18}$.
(2)$\frac{3}{5}\sqrt{xy^{2}}\div(-\frac{4}{15}\sqrt{\frac{y}{x}})\cdot(-\frac{5}{6}\sqrt{x^{3}y})$.
答案:
解析
(1)原式 $=3\sqrt{\frac{5}{4}}\div\frac{3}{4}\sqrt{\frac{5}{2}}\times2\sqrt{18}$ $=3\sqrt{\frac{5}{4}}\times\frac{4}{3}\sqrt{\frac{2}{5}}\times2\sqrt{18}$ $=3\times\frac{4}{3}\times2\times\sqrt{\frac{5}{4}\times\frac{2}{5}\times18}=24$。
(2)原式 $=\frac{3}{5}\sqrt{xy^{2}}\cdot(-\frac{15}{4}\sqrt{\frac{x}{y}})\cdot(-\frac{5}{6}\sqrt{x^{3}y})$ $=(\frac{3}{5}\times\frac{15}{4}\times\frac{5}{6})\cdot\sqrt{xy^{2}\cdot\frac{x}{y}\cdot x^{3}y}$ $=\frac{15}{8}\sqrt{x^{5}y^{2}}=\frac{15}{8}\sqrt{x^{4}y^{2}}\cdot\sqrt{x}=\frac{15}{8}x^{2}y\sqrt{x}$。
(1)原式 $=3\sqrt{\frac{5}{4}}\div\frac{3}{4}\sqrt{\frac{5}{2}}\times2\sqrt{18}$ $=3\sqrt{\frac{5}{4}}\times\frac{4}{3}\sqrt{\frac{2}{5}}\times2\sqrt{18}$ $=3\times\frac{4}{3}\times2\times\sqrt{\frac{5}{4}\times\frac{2}{5}\times18}=24$。
(2)原式 $=\frac{3}{5}\sqrt{xy^{2}}\cdot(-\frac{15}{4}\sqrt{\frac{x}{y}})\cdot(-\frac{5}{6}\sqrt{x^{3}y})$ $=(\frac{3}{5}\times\frac{15}{4}\times\frac{5}{6})\cdot\sqrt{xy^{2}\cdot\frac{x}{y}\cdot x^{3}y}$ $=\frac{15}{8}\sqrt{x^{5}y^{2}}=\frac{15}{8}\sqrt{x^{4}y^{2}}\cdot\sqrt{x}=\frac{15}{8}x^{2}y\sqrt{x}$。
20.(8分)
(1)实数$a$,$b$在数轴上对应的点的位置如图所示,化简:$\sqrt{a^{2}}-\sqrt{b^{2}}-\sqrt{(a - b)^{2}}$.
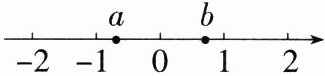
(2)已知$4 < a < 11$,化简:$\sqrt{(a - 4)^{2}}+\sqrt{(a - 11)^{2}}$.
(1)实数$a$,$b$在数轴上对应的点的位置如图所示,化简:$\sqrt{a^{2}}-\sqrt{b^{2}}-\sqrt{(a - b)^{2}}$.
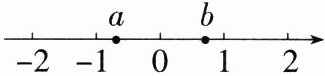
(2)已知$4 < a < 11$,化简:$\sqrt{(a - 4)^{2}}+\sqrt{(a - 11)^{2}}$.
答案:
解析
(1)由数轴知,$a<0<b$,$\therefore a - b<0$,$\therefore\sqrt{a^{2}}-\sqrt{b^{2}}-\sqrt{(a - b)^{2}}=\vert a\vert-\vert b\vert-\vert a - b\vert=(-a)-b+a - b=-2b$。
(2)$\because4<a<11$,$\therefore a - 4>0$,$a - 11<0$,$\therefore\sqrt{(a - 4)^{2}}+\sqrt{(a - 11)^{2}}=\vert a - 4\vert+\vert a - 11\vert=a - 4+11 - a=7$。
(1)由数轴知,$a<0<b$,$\therefore a - b<0$,$\therefore\sqrt{a^{2}}-\sqrt{b^{2}}-\sqrt{(a - b)^{2}}=\vert a\vert-\vert b\vert-\vert a - b\vert=(-a)-b+a - b=-2b$。
(2)$\because4<a<11$,$\therefore a - 4>0$,$a - 11<0$,$\therefore\sqrt{(a - 4)^{2}}+\sqrt{(a - 11)^{2}}=\vert a - 4\vert+\vert a - 11\vert=a - 4+11 - a=7$。
21.(8分)数学课上,邱老师在黑板上给出了如下等式.
第1个等式:
$\frac{1}{\sqrt{2}-1}=\frac{\sqrt{2}+1}{(\sqrt{2}-1)(\sqrt{2}+1)}=\frac{\sqrt{2}+1}{2 - 1}=\sqrt{2}+1$;
第2个等式:
$\frac{1}{\sqrt{3}-\sqrt{2}}=\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}=\frac{\sqrt{3}+\sqrt{2}}{3 - 2}=\sqrt{3}+\sqrt{2}$;……
请你根据上述方法完成下列题目:
(1)计算:$\frac{1}{\sqrt{5}-\sqrt{4}}=$________.
(2)比较$\frac{1}{\sqrt{n + 1}-\sqrt{n}}$与$\frac{1}{\sqrt{n}-\sqrt{n - 1}}$的大小($n\geqslant2$,且$n$为正整数).
第1个等式:
$\frac{1}{\sqrt{2}-1}=\frac{\sqrt{2}+1}{(\sqrt{2}-1)(\sqrt{2}+1)}=\frac{\sqrt{2}+1}{2 - 1}=\sqrt{2}+1$;
第2个等式:
$\frac{1}{\sqrt{3}-\sqrt{2}}=\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}=\frac{\sqrt{3}+\sqrt{2}}{3 - 2}=\sqrt{3}+\sqrt{2}$;……
请你根据上述方法完成下列题目:
(1)计算:$\frac{1}{\sqrt{5}-\sqrt{4}}=$________.
(2)比较$\frac{1}{\sqrt{n + 1}-\sqrt{n}}$与$\frac{1}{\sqrt{n}-\sqrt{n - 1}}$的大小($n\geqslant2$,且$n$为正整数).
答案:
解析
(1)$\frac{1}{\sqrt{5}-\sqrt{4}}=\frac{\sqrt{5}+\sqrt{4}}{(\sqrt{5}-\sqrt{4})(\sqrt{5}+\sqrt{4})}=\frac{\sqrt{5}+\sqrt{4}}{5 - 4}=\sqrt{5}+2$。
(2)$\frac{1}{\sqrt{n + 1}-\sqrt{n}}=\frac{\sqrt{n + 1}+\sqrt{n}}{(\sqrt{n + 1}-\sqrt{n})(\sqrt{n + 1}+\sqrt{n})}=\frac{\sqrt{n + 1}+\sqrt{n}}{n + 1 - n}=\sqrt{n + 1}+\sqrt{n}$, $\frac{1}{\sqrt{n}-\sqrt{n - 1}}=\frac{\sqrt{n}+\sqrt{n - 1}}{(\sqrt{n}-\sqrt{n - 1})(\sqrt{n}+\sqrt{n - 1})}=\frac{\sqrt{n}+\sqrt{n - 1}}{n-(n - 1)}=\sqrt{n}+\sqrt{n - 1}$。 $\because\sqrt{n + 1}>\sqrt{n - 1}$,$\therefore\sqrt{n + 1}+\sqrt{n}>\sqrt{n}+\sqrt{n - 1}$,$\therefore\frac{1}{\sqrt{n + 1}-\sqrt{n}}>\frac{1}{\sqrt{n}-\sqrt{n - 1}}$。
(1)$\frac{1}{\sqrt{5}-\sqrt{4}}=\frac{\sqrt{5}+\sqrt{4}}{(\sqrt{5}-\sqrt{4})(\sqrt{5}+\sqrt{4})}=\frac{\sqrt{5}+\sqrt{4}}{5 - 4}=\sqrt{5}+2$。
(2)$\frac{1}{\sqrt{n + 1}-\sqrt{n}}=\frac{\sqrt{n + 1}+\sqrt{n}}{(\sqrt{n + 1}-\sqrt{n})(\sqrt{n + 1}+\sqrt{n})}=\frac{\sqrt{n + 1}+\sqrt{n}}{n + 1 - n}=\sqrt{n + 1}+\sqrt{n}$, $\frac{1}{\sqrt{n}-\sqrt{n - 1}}=\frac{\sqrt{n}+\sqrt{n - 1}}{(\sqrt{n}-\sqrt{n - 1})(\sqrt{n}+\sqrt{n - 1})}=\frac{\sqrt{n}+\sqrt{n - 1}}{n-(n - 1)}=\sqrt{n}+\sqrt{n - 1}$。 $\because\sqrt{n + 1}>\sqrt{n - 1}$,$\therefore\sqrt{n + 1}+\sqrt{n}>\sqrt{n}+\sqrt{n - 1}$,$\therefore\frac{1}{\sqrt{n + 1}-\sqrt{n}}>\frac{1}{\sqrt{n}-\sqrt{n - 1}}$。
查看更多完整答案,请扫码查看


