《2025年5年中考3年模拟八年级数学下册人教版》

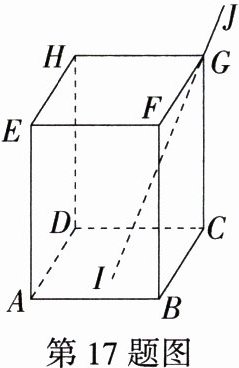
17.如图,在长方体ABCD - EFGH盒子中,已知AB = 4 cm,BC = 3 cm,CG = 5 cm,长为10 cm的细直木棒IJ恰好从小孔G处插入,木棒的一端I与底面ABCD接触,当木棒的端点I在长方形ABCD内及边界运动时,GJ的长度最小为________cm.

答案： 答案：$(10 - 5\sqrt{2})$ 解析：当$GI$最长时，$GJ$最短，当$I$运动到点$A$时，$GI$最长，连接$AC$（图略），此时$GI=\sqrt{AC^{2}+CG^{2}}$，因为$AC^{2}=AB^{2}+BC^{2}=4^{2}+3^{2}=25$，所以$GI=\sqrt{25 + 5^{2}}=\sqrt{50}=5\sqrt{2}(cm)$，所以$GJ$的长度最小为$(10 - 5\sqrt{2})cm$。

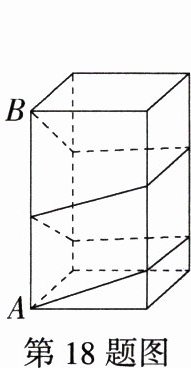
18.如图,长方体的底面是边长为2 cm的正方形,高为6 cm.如果用细线从点A开始经过4个侧面缠绕2圈到达B,那么所用细线最短需要________cm.

答案：
答案：$2\sqrt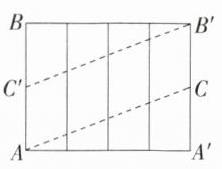{73}$ 解析：
如图，将长方体的侧面沿$AB$展开，取$A'B'$的中点$C$，取$AB$的中点$C'$，连接$B'C'$，$AC$，则$AC + B'C'$的值为所求的最短细线长，因为$AC^{2}=AA'^{2}+A'C^{2}$，$AA'=2\times4 = 8(cm)$，$A'C=\frac{1}{2}\times6 = 3(cm)$，所以$AC=\sqrt{73}cm$，同理，$B'C'=\sqrt{73}cm$，所以$AC + B'C'=2\sqrt{73}cm$。故所用细线最短需要$2\sqrt{73}cm$。

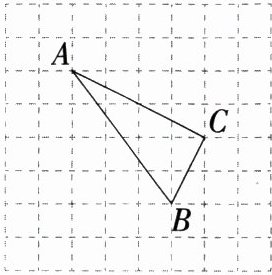
19.(2024广东江门月考)(6分)如图,方格纸中小正方形的边长均为1个单位长度,△ABC为格点三角形.
(1)建立平面直角坐标系,使点A的坐标为(-5,4),点B的坐标为(-2,0),此时点C的坐标为________.
(2)判断△ABC的形状,并说明理由.

答案：
解析：\n（1）如图，点$C$的坐标为$(-1,2)$。
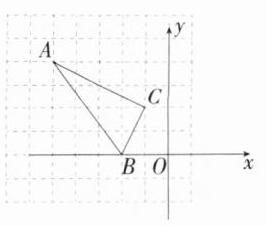
（2）$\triangle ABC$是直角三角形。理由如下：因为$AB^{2}=3^{2}+4^{2}=25$，$BC^{2}=1^{2}+2^{2}=5$，$AC^{2}=2^{2}+4^{2}=20$，所以$AB^{2}=BC^{2}+AC^{2}$，所以$\triangle ABC$是直角三角形。

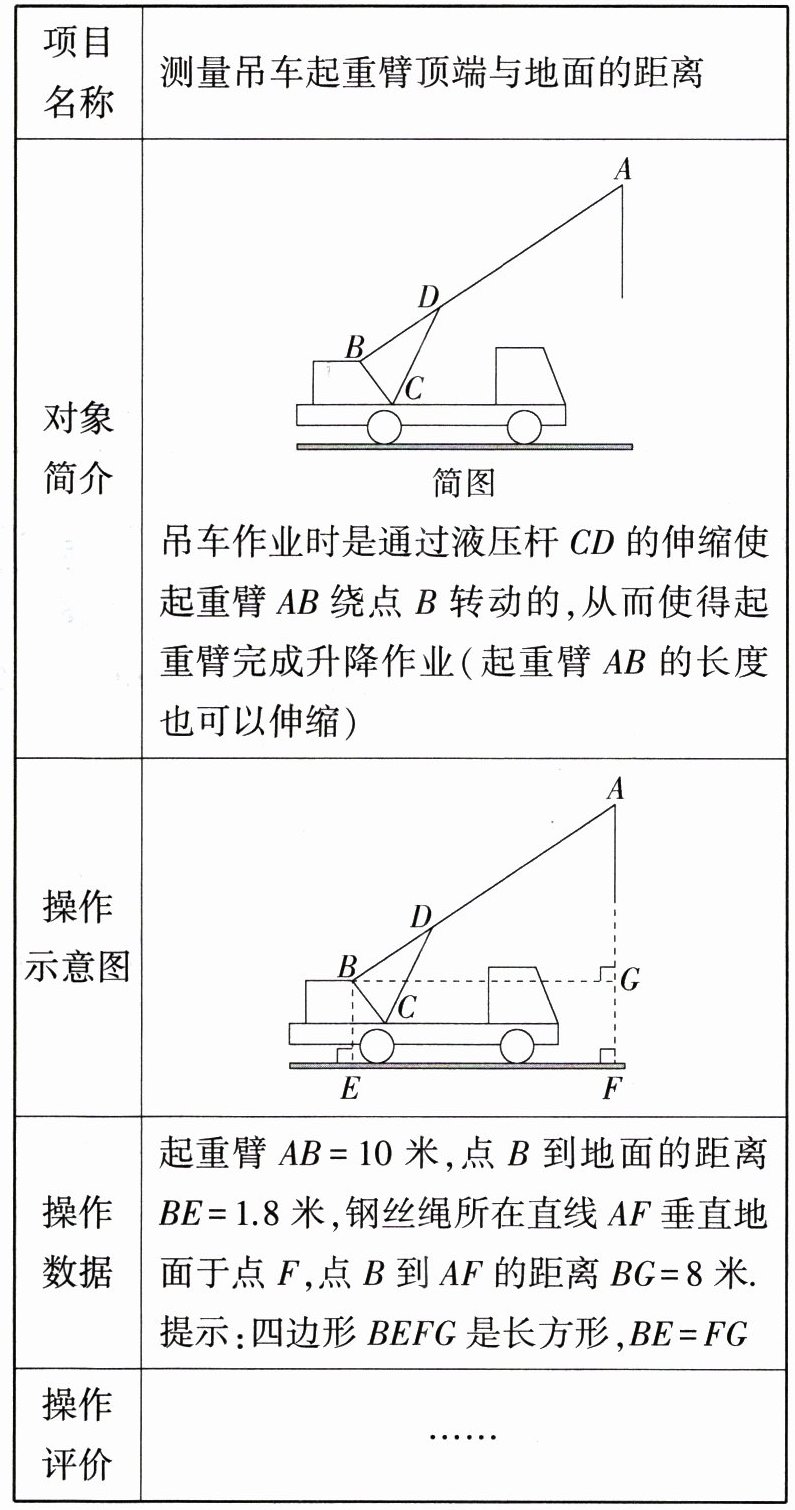
20.新考向·项目式学习试题 (2023山东济南期末)(6分)某初中数学小组欲测量吊车起重臂顶端与地面的距离,下面是他们设计的项目课题,请你根据下面的表格计算：吊车起重臂的顶端A到地面的距离AF.

答案： 解析：在$Rt\triangle ABG$中，由勾股定理得$AG=\sqrt{AB^{2}-BG^{2}}=\sqrt{10^{2}-8^{2}} = 6$（米），因为$FG = BE = 1.8$米，所以$AF=AG + GF=6 + 1.8 = 7.8$（米）。答：点$A$到地面的距离$AF$为$7.8$米。