《2025年5年中考3年模拟八年级数学下册人教版》

20.（2023浙江绍兴中考，22，★★☆）如图，在正方形ABCD中，G是对角线BD上的一点（与点B，D不重合），GE⊥CD，GF⊥BC，E，F分别为垂足. 连接EF，AG，并延长AG交EF于点H.
（1）求证：∠DAG = ∠EGH.
（2）判断AH与EF是否垂直，并说明理由.

答案：
解析： （1）证明：因为四边形ABCD是正方形，所以AD⊥CD，因为GE⊥CD，所以AD//GE，所以∠DAG = ∠EGH。 （2）AH⊥EF。理由如下：连接GC交EF于点O，如图，因为BD为正方形ABCD的对角线，所以∠ADG = ∠CDG = 45°，因为DG = DG，AD = CD，所以△ADG≌△CDG(SAS)，所以∠DAG = ∠DCG。在正方形ABCD中，∠ECF = 90°，因为GE⊥CD，GF⊥BC，所以四边形FCEG为矩形，所以OE = OC，所以∠OEC = ∠OCE，所以∠DAG = ∠OEC，由（1）得∠DAG = ∠EGH，所以∠EGH = ∠OEC，所以∠EGH + ∠GEH = ∠OEC + ∠GEH = ∠GEC = 90°，所以∠GHE = 90°，所以AH⊥EF。

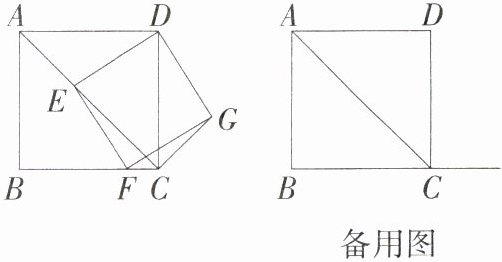
21. 推理能力（2024浙江杭州期末）如图，四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG.
（1）求证：矩形DEFG是正方形.
（2）若AB = 3，CE = 2$\sqrt{2}$，求CG的长度.
（3）当线段DE与正方形ABCD的某条边的夹角是30°时，求∠EFC的度数.

答案：
解析： （1）证明：如图1，过E作EP⊥CD于P，EQ⊥BC于Q，因为四边形ABCD是正方形，所以∠DCA = ∠BCA = 45°，所以EQ = EP，因为∠QEF + ∠PEF = 90°，∠PED + ∠PEF = 90°，所以∠QEF = ∠PED，在△EQF和△EPD中，{∠QEF = ∠PED，EQ = EP，∠EQF = ∠EPD}，所以△EQF≌△EPD(ASA)，所以EF = ED，所以矩形DEFG是正方形。（2）因为四边形ABCD是正方形，AB = 3，所以AD = CD = AB = 3，∠ADC = 90°，所以AC = √(AD² + CD²) = 3√2，因为CE = 2√2，所以AE = √2，因为四边形DEFG是正方形，所以DE = DG，∠EDG = 90° = ∠ADC，所以∠ADE = ∠CDG，所以△ADE≌△CDG(SAS)，所以CG = AE = √2。 （3）①当DE与AD的夹角为30°时，如图2，因为∠ADE = 30°，∠ADC = 90°，所以∠EDC = 60°，因为∠EDC + ∠DEF + ∠EFC + ∠FCD = 360°，所以∠EFC = 360° - 90° - 90° - 60° = 120°； ②当DE与DC的夹角为30°时，如图3，因为∠EDC = 30°，∠DCA = 45°，所以∠DEC = 180° - 30° - 45° = 105°，因为∠DEF = 90°，所以∠CEF = 105° - 90° = 15°，所以∠EFC = ∠ACB - ∠CEF = 30°。 综上所述，∠EFC = 30°或120°。 

22. 几何直观 将一张矩形纸片ABCD按照下面步骤进行折叠：
第一步：如图①，将矩形纸片沿AM折叠，使得点D的对应点N落在AB上，连接MN，然后把纸片展开，得到折痕AM.
第二步：如图②，将四边形ADMN沿PQ对折，使AD与NM重合. 将纸片展开，得到折痕PQ，然后连接NQ.
第三步：如图③，折叠纸片使得NQ落在DC上，折痕为EQ，点N的对应点为F.
（1）求证：四边形ADMN是正方形.
（2）求图③中四边形NQFE的面积与四边形ADMN的面积的比值.

答案： 解析： （1）证明：因为四边形ABCD是矩形，所以∠DAN = ∠D = 90°，由折叠可得∠ANM = ∠D = 90°，AD = AN，所以四边形ADMN是正方形。 （2）因为四边形ADMN为正方形，所以AD = DM = MN，设AD = DM = MN = 2a，因为将正方形ADMN对折后，AD与NM重合，所以DQ = QM = a，在Rt△NQM中，由勾股定理得NQ = √(QM² + NM²) = √(a² + (2a)²) = √5a，由折叠可得QF = NQ = √5a，易证四边形NQFE为菱形，因为四边形NQFE的QF边上的高与四边形ADMN的DM边上的高都是2a，所以S四边形NQFE : S四边形ADMN = QF : DM = √5a : 2a = √5/2。