《2025年5年中考3年模拟八年级数学下册人教版》

15. [分类讨论思想] (2021黑龙江齐齐哈尔中考,15,★★☆)直角三角形的两条边长分别为3和4，则这个直角三角形斜边上的高为__________.

答案： 答案：$\frac{12}{5}$或$\frac{3\sqrt{7}}{4}$ 解析：设直角三角形斜边上的高为h， ①当4是直角边长时，斜边长$=\sqrt{3^{2}+4^{2}} = 5$，则$\frac{1}{2}×3×4=\frac{1}{2}×5×h$，解得$h=\frac{12}{5}$； ②当4是斜边长时，3为一直角边长，则另一直角边长$=\sqrt{4^{2}-3^{2}}=\sqrt{7}$，则$\frac{1}{2}×3×\sqrt{7}=\frac{1}{2}×4×h$，解得$h=\frac{3\sqrt{7}}{4}$。 综上所述，这个直角三角形斜边上的高为$\frac{12}{5}$或$\frac{3\sqrt{7}}{4}$。

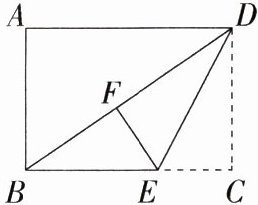
16. [方程思想] (2023广东深圳福田外国语学校期末,16,★★☆)如图，在长方形ABCD中，AB = 6，AD = 8，点E在BC边上，将△DCE沿DE折叠，使点C恰好落在对角线BD上的点F处，则CE的长为________.(M8217001)

答案： 答案：3 解析：因为四边形ABCD为长方形，所以$CD = AB = 6$，$BC = AD = 8$，$\angle DCB = 90^{\circ}$，所以在Rt$\triangle BCD$中，$BD=\sqrt{CD^{2}+BC^{2}} = 10$，由折叠可知$\angle DFE=\angle DCB = 90^{\circ}$，$DF = DC = 6$，$EF = EC$，所以$\angle BFE = 180^{\circ}-\angle DFE = 90^{\circ}$，$BF = BD - DF = 4$，设$EC = EF = x$，则$BE = 8 - x$，在Rt$\triangle BEF$中，由勾股定理得$BE^{2}=EF^{2}+BF^{2}$，所以$(8 - x)^{2}=x^{2}+4^{2}$，解得$x = 3$，即$CE = 3$。

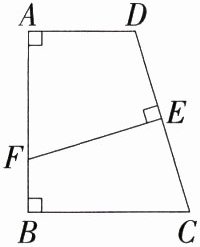
17. (2024山东德州月考,21,★★☆)如图，在四边形ABCD中，∠A = ∠B = 90°，边CD的垂直平分线分别交CD，AB于E，F.若AD = 4，AB = 7，BC = 6，求BF的长.

答案：
解析：如图，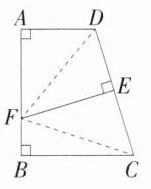
连接DF，CF，因为EF垂直平分CD，所以$DF = CF$。设$BF = x$，则$AF = 7 - x$，在Rt$\triangle ADF$和Rt$\triangle BCF$中，$AD^{2}+AF^{2}=DF^{2}=CF^{2}=BC^{2}+BF^{2}$，所以$4^{2}+(7 - x)^{2}=6^{2}+x^{2}$，解得$x=\frac{29}{14}$，所以$BF=\frac{29}{14}$。

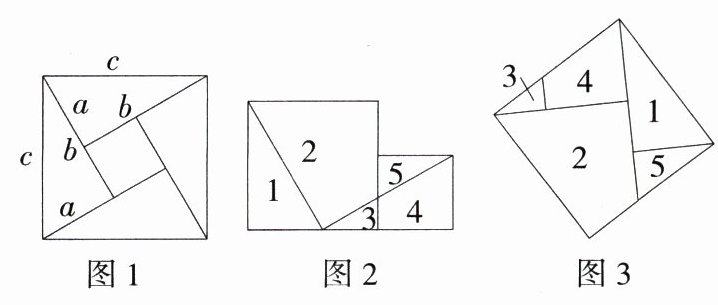
18. (2024陕西延安月考,25,★★☆)如图1，我们称该图案为“赵爽弦图”.“赵爽弦图”由四个全等的直角三角形围成一个大正方形，中间的部分是一个小正方形，其中直角三角形的两直角边长分别为a，b(b ＞ a ＞ 0)，斜边长为c.(M8217001)
(1)请利用图1验证勾股定理.
(2)在图1中，若c = 15，b = 12，求小正方形的面积.
(3)小明按如图2所示的方式把边长为3 cm和2 cm的两个正方形切割成5块，按如图3所示的方式无缝拼成一个大正方形，求大正方形的边长.

答案： 解析：（1）因为大正方形的面积 = 小正方形的面积 + 四个直角三角形的面积，所以$c^{2}=(b - a)^{2}+4×\frac{1}{2}ab=b^{2}-2ab + a^{2}+2ab=b^{2}+a^{2}$，即$a^{2}+b^{2}=c^{2}$。 （2）由勾股定理得$a=\sqrt{c^{2}-b^{2}}=\sqrt{15^{2}-12^{2}} = 9$，所以小正方形的面积$=(12 - 9)^{2}=9$。 （3）因为大正方形的面积为$3^{2}+2^{2}=9 + 4 = 13$ ($cm^{2}$)，所以大正方形的边长为$\sqrt{13}$ cm。

19. (2024江西宜春月考,20,★★☆)定义：我们把三角形某边上的中点到这条边上的高的距离称为三角形某边的“中偏度值”.
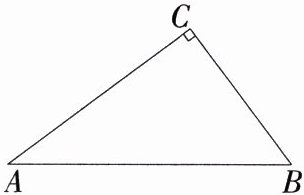
(1)如图，在Rt△ABC中，∠ACB = 90°，AC = 4，BC = 3，求△ABC中AB边的“中偏度值”.
(2)在△ABC中，AC = 13，AB = 15，BC边上的高AD = 12，求△ABC中BC边的“中偏度值”.

答案：
解析：（1）如图，作Rt$\triangle ABC$中AB边上的中线CE和高CD，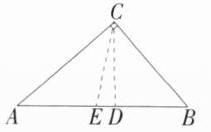
因为$\angle ACB = 90^{\circ}$，$AC = 4$，$BC = 3$，所以$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{4^{2}+3^{2}} = 5$，因为$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$，所以$\frac{1}{2}×4×3=\frac{1}{2}×5×CD$，所以$CD=\frac{12}{5}$，所以$BD=\sqrt{BC^{2}-CD^{2}}=\sqrt{3^{2}-(\frac{12}{5})^{2}}=\frac{9}{5}$，因为CE为Rt$\triangle ABC$斜边AB上的中线，$AB = 5$，所以$BE=\frac{1}{2}AB=\frac{5}{2}$，所以$ED = BE - BD=\frac{5}{2}-\frac{9}{5}=\frac{7}{10}$，所以$\triangle ABC$中AB边的“中偏度值”为$\frac{7}{10}$。 （2）①当高AD在$\triangle ABC$内部时，作$\triangle ABC$中BC边上的中线AE，如图，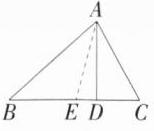
因为$AD\perp BC$，$AD = 12$，$AC = 13$，$AB = 15$，所以$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{13^{2}-12^{2}} = 5$，$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{15^{2}-12^{2}} = 9$，所以$BC = BD + CD = 14$，因为AE为$\triangle ABC$中BC边上的中线，所以$CE=\frac{1}{2}BC = 7$，所以$ED = CE - CD = 7 - 5 = 2$，所以$\triangle ABC$中BC边的“中偏度值”为2； ②当高AD在$\triangle ABC$外部时，作$\triangle ABC$中BC边上的中线AE，如图，
因为$AD\perp BC$，$AD = 12$，$AC = 13$，$AB = 15$，所以$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{13^{2}-12^{2}} = 5$，$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{15^{2}-12^{2}} = 9$，所以$BC = BD - CD = 4$，因为AE为$\triangle ABC$中BC边上的中线，所以$CE=\frac{1}{2}BC = 2$，所以$ED = CE + CD = 2 + 5 = 7$，所以$\triangle ABC$中BC边的“中偏度值”为7。 综上所述，$\triangle ABC$中BC边的“中偏度值”为2或7。