《2025年5年中考3年模拟八年级数学下册人教版》

6.(2024内蒙古通辽中考，9，★☆☆)如图，□ABCD的对角线AC，BD交于点O，以下条件不能证明□ABCD是菱形的是(M8218006) ( )

A.∠BAC = ∠BCA
B.∠ABD = ∠CBD
C.OA²+OB² = AD²
D.AD²+OA² = OD²

答案： D - A. 因为∠BAC = ∠BCA，所以AB = BC，所以□ABCD是菱形，故选项A不符合题意；\nB. 因为四边形ABCD是平行四边形，所以AD//BC，所以∠ADB = ∠CBD，因为∠ABD = ∠CBD，所以∠ABD = ∠ADB，所以AB = AD，所以□ABCD是菱形，故选项B不符合题意；\nC. 因为四边形ABCD是平行四边形，所以OB = OD，因为OA² + OB² = AD²，所以OA² + OD² = AD²，所以∠AOD = 90°，所以AC⊥BD，所以□ABCD是菱形，故选项C不符合题意；\nD. 因为AD² + OA² = OD²，所以∠OAD = 90°，所以OA⊥AD，所以不能证得□ABCD是菱形，故选项D符合题意。故选D。

7.(2023广东深圳中考，5，★☆☆)如图，在平行四边形ABCD中，AB = 4，BC = 6，将线段AB水平向右平移a个单位长度得到线段FE，若四边形ECDF为菱形，则a的值为 ( )

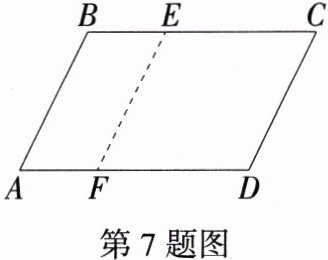
A.1
B.2
C.3
D.4

答案： B 因为四边形ABCD是平行四边形，所以AB//CD，CE//FD，CD = AB = 4，因为将线段AB水平向右平移得到线段FE，所以AB//EF//CD，所以四边形ECDF为平行四边形，当CE = CD = 4时，□ECDF为菱形，所以a = BE = BC - CE = 6 - 4 = 2。故选B。

8.(2023黑龙江齐齐哈尔中考，12，★☆☆)如图，在四边形ABCD中，AD = BC，AC⊥BD于点O.请添加一个条件：________，使四边形ABCD成为菱形.

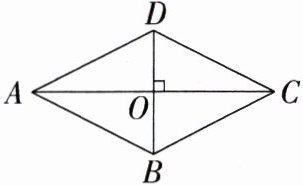
答案： AD//BC（答案不唯一） 解析：当添加AD//BC时，因为AD = BC，所以四边形ABCD是平行四边形，因为AC⊥BD，所以四边形ABCD是菱形。（答案不唯一）

9.(2024河北沧州期末，21，★★☆)如图，∠BAC = 90°，AD是△ABC的中线，AF//BC，BF与AD交于点E，且点E恰好是BF的中点，连接CF.
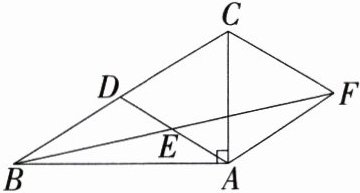
(1)求证：四边形ADCF是菱形.
(2)若∠DCF = 120°，AC = 8，求菱形ADCF的周长.

答案： - （1）证明：因为AD是△ABC的中线，所以点D是BC的中点，又因为点E是BF的中点，所以DE//CF，即DA//CF，因为AF//BC，所以四边形ADCF是平行四边形，因为AD是△ABC的中线，∠BAC = 90°，所以CD = BD = AD，所以四边形ADCF是菱形。\n（2）因为四边形ADCF是菱形，∠DCF = 120°，所以∠ACD = ∠ACF = 60°，因为AD = DC，所以△ACD是等边三角形，所以AD = DC = AC = 8，所以菱形ADCF的周长为8×4 = 32。

10.(2021湖北十堰中考，21，★★☆)如图，已知在△ABC中，D是AC的中点，过点D作DE⊥AC交BC于点E，过点A作AF//BC交直线DE于点F，连接AE、CF.
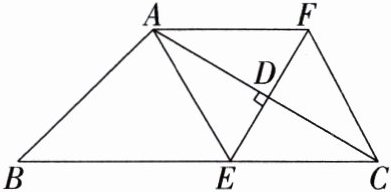
(1)求证：四边形AECF是菱形.
(2)若CF = 2，∠FAC = 30°，∠B = 45°，求AB的长.

答案：
- （1）证明：因为点D是AC的中点，所以AD = CD，因为AF//BC，所以∠FAD = ∠ECD，∠AFD = ∠CED，所以△AFD≌△CED（AAS），所以AF = CE，所以四边形AECF是平行四边形，因为EF⊥AC，所以四边形AECF是菱形。\n（2）如图，过点A作AG⊥BC于点G，由（1）知四边形AECF是菱形，所以AE = CF = 2，∠FAE = 2∠FAC = 60°，因为AF//BC，所以∠AEG = ∠FAE = 60°，因为AG⊥BC，所以∠AGB = ∠AGE = 90°，所以∠GAE = 30°，所以GE = $\frac{1}{2}$AE = 1，所以AG = $\sqrt{AE^{2}-GE^{2}}$ = $\sqrt{3}$，因为∠B = 45°，所以∠GAB = 45° = ∠B，所以BG = AG = $\sqrt{3}$，所以AB = $\sqrt{BG^{2}+AG^{2}}$ = $\sqrt{6}$。

11.运算能力 已知△ABC和△DEF都是边长为10 cm的等边三角形，且B、D、C、E在同一直线上，连接AD、CF，已知BD = 3 cm，若△ABC沿着BE方向以1 cm/s的速度运动，设△ABC的运动时间为t s.
(1)当t为何值时，四边形ADFC是菱形?
(2)当t为何值时，四边形ADFC是矩形? 并求其面积.
(3)当t为何值时，四边形ADFC的面积是100√3 cm²?

答案： - （1）因为△ABC和△DEF都是边长为10 cm的等边三角形，所以AC = DF，∠ACD = ∠FDE = 60°，所以AC//DF，所以四边形ADFC是平行四边形，当t = 3时，点B与点D重合，所以AD = DF，所以四边形ADFC是菱形。故当t = 3时，四边形ADFC是菱形。\n（2）由（1）知四边形ADFC为平行四边形，当t = 13时，点B与点E重合，此时A、E、F在同一条直线上，所以AF = CD，所以四边形ADFC是矩形，所以∠CFD = 90°，所以CF = $\sqrt{CD^{2}-DF^{2}}$ = 10$\sqrt{3}$ cm，所以S＜sub＞矩形ADFC＜/sub＞ = 10×10$\sqrt{3}$ = 100$\sqrt{3}$（cm＜sup＞2＜/sup＞）。故当t = 13时，四边形ADFC是矩形，其面积为100$\sqrt{3}$ cm＜sup＞2＜/sup＞。\n（3）由题意知CD = (7 + t)cm，过A作AM⊥BC于点M（图略），则BM = $\frac{1}{2}$BC = 5 cm，所以AM = $\sqrt{AB^{2}-BM^{2}}$ = 5$\sqrt{3}$ cm，所以S＜sub＞四边形ADFC＜/sub＞ = 2S＜sub＞△ADC＜/sub＞ = CD·AM，所以(7 + t)×5$\sqrt{3}$ = 100$\sqrt{3}$，解得t = 13。故当t = 13时，四边形ADFC的面积是100$\sqrt{3}$ cm＜sup＞2＜/sup＞。