第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
4.如图1,菱形ABCD的对角线AC、BD相交于点O,且AC = 6 cm,BD = 8 cm,分别过点B、C作AC与BD的平行线相交于点E.
(1)判断四边形BOCE的形状,并证明.
(2)点G从点A沿线段AC的方向以2 cm/s的速度移动了t s,连接BG,当S_{△ABG}=2S_{△OBG}时,求t的值.
(3)如图2,点G在直线AC上运动,求BG + EG的最小值.


(1)判断四边形BOCE的形状,并证明.
(2)点G从点A沿线段AC的方向以2 cm/s的速度移动了t s,连接BG,当S_{△ABG}=2S_{△OBG}时,求t的值.
(3)如图2,点G在直线AC上运动,求BG + EG的最小值.


答案:
(1)四边形$BOCE$是矩形。证明:因为$BE// OC$,$EC// OB$,所以四边形$BOCE$是平行四边形,因为四边形$ABCD$是菱形,所以$AC\perp BD$,所以$\angle BOC = 90^{\circ}$,所以四边形$BOCE$是矩形。(2)因为四边形$ABCD$是菱形,$AC = 6\mathrm{cm}$,所以$OA = OC = 3\mathrm{cm}$,因为$S_{\triangle ABC}=2S_{\triangle OBC}$,所以$AG = 2OG$,所以$2t = 2(3 - 2t)$或$2t = 2(2t - 3)$,解得$t = 1$或$t = 3$,所以满足条件的$t$的值为$1$或$3$。(3)因为四边形$ABCD$是菱形,所以$OB = OD$,$AC\perp BD$,因为四边形$BOCE$是矩形,所以$BE = OC = 3\mathrm{cm}$,$\angle EBO = 90^{\circ}$,连接$ED$,交$AC$于点$H$,连接$DG$,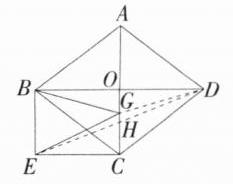
则$BG = DG$,所以$BG + EG = DG + EG\geq DE$,所以当$E$,$G$,$D$三点共线,即点$G$与点$H$重合时,$BG + EG$有最小值,即线段$DE$的长,在$Rt\triangle EBD$中,$DE=\sqrt{BE^{2}+BD^{2}}=\sqrt{3^{2}+8^{2}}=\sqrt{73}(\mathrm{cm})$,所以$BG + EG$的最小值为$\sqrt{73}\mathrm{cm}$。
(1)四边形$BOCE$是矩形。证明:因为$BE// OC$,$EC// OB$,所以四边形$BOCE$是平行四边形,因为四边形$ABCD$是菱形,所以$AC\perp BD$,所以$\angle BOC = 90^{\circ}$,所以四边形$BOCE$是矩形。(2)因为四边形$ABCD$是菱形,$AC = 6\mathrm{cm}$,所以$OA = OC = 3\mathrm{cm}$,因为$S_{\triangle ABC}=2S_{\triangle OBC}$,所以$AG = 2OG$,所以$2t = 2(3 - 2t)$或$2t = 2(2t - 3)$,解得$t = 1$或$t = 3$,所以满足条件的$t$的值为$1$或$3$。(3)因为四边形$ABCD$是菱形,所以$OB = OD$,$AC\perp BD$,因为四边形$BOCE$是矩形,所以$BE = OC = 3\mathrm{cm}$,$\angle EBO = 90^{\circ}$,连接$ED$,交$AC$于点$H$,连接$DG$,

则$BG = DG$,所以$BG + EG = DG + EG\geq DE$,所以当$E$,$G$,$D$三点共线,即点$G$与点$H$重合时,$BG + EG$有最小值,即线段$DE$的长,在$Rt\triangle EBD$中,$DE=\sqrt{BE^{2}+BD^{2}}=\sqrt{3^{2}+8^{2}}=\sqrt{73}(\mathrm{cm})$,所以$BG + EG$的最小值为$\sqrt{73}\mathrm{cm}$。
5.点O为正方形ABCD对角线AC与BD的交点,点E为直线BD上一点(点E与点B,点D,点O不重合),连接AE.
(1)如图1,若点E为OD的中点,AB = $\sqrt{2}$,求△ABE的面积.
(2)如图2,若点E在线段OD上,过点E作EF⊥AE交直线BC于点F,交直线AC于点H,过点F作FG//AE交直线BD于点G.求证:FG + FH = AE.
(3)若点E为直线BD上一动点,其他条件与第(2)问条件相同,请写出线段DE,BG,CH之间的数量关系.

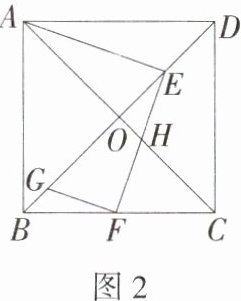
(1)如图1,若点E为OD的中点,AB = $\sqrt{2}$,求△ABE的面积.
(2)如图2,若点E在线段OD上,过点E作EF⊥AE交直线BC于点F,交直线AC于点H,过点F作FG//AE交直线BD于点G.求证:FG + FH = AE.
(3)若点E为直线BD上一动点,其他条件与第(2)问条件相同,请写出线段DE,BG,CH之间的数量关系.


答案:
(1)因为四边形$ABCD$为正方形,$AB=\sqrt{2}$,所以$OA = OB = OD = 1$,$AO\perp BD$,因为点$E$为$OD$的中点,所以$OE=\frac{1}{2}OD=\frac{1}{2}$,所以$BE = BO + OE=\frac{3}{2}$,所以$S_{\triangle ABE}=\frac{1}{2}BE\cdot AO=\frac{1}{2}\times\frac{3}{2}\times1=\frac{3}{4}$。
(2)证明:过点$E$作直线$EN\perp BC$于点$N$,交$AD$于$M$,
易知四边形$AMNB$为矩形,所以$AM = BN$,$\angle AME=\angle AEF=\angle FNE = 90^{\circ}$,在正方形$ABCD$中,$\angle EBN = 45^{\circ}$,所以$EN = BN = AM$,因为$\angle MAE+\angle1=\angle FEN+\angle1 = 90^{\circ}$,所以$\angle MAE=\angle FEN$,所以$\triangle AME\cong\triangle ENF(ASA)$,所以$AE = EF$,同理可得,$\triangle AHE\cong\triangle EGF$,所以$FG = EH$,因为$EH + FH = EF = AE$,所以$FG + FH = AE$。
(3)①当点$E$在线段$OD$上时,由(2)得$\triangle AHE\cong\triangle EGF$,所以$AH = EG$,因为$AH = AC - CH$,$EG = BD - BG - DE$,$AC = BD$,所以$AC - CH = BD - BG - DE$,即$CH = BG + DE$。
②当点$E$在线段$DB$的延长线上时,连接$CE$,
因为四边形$ABCD$是正方形,所以$BD$垂直平分$AC$,$\angle BAO=\angle BCO = 45^{\circ}$,所以$AE = CE$,所以$\angle EAO=\angle ECO$,所以$\angle EAO-\angle BAO=\angle ECO-\angle BCO$,所以$\angle EAB=\angle ECB$,在$Rt\triangle FME$和$Rt\triangle AMB$中,由“$8$”字型得$\angle MAB=\angle MFE$,所以$\angle MFE=\angle ECB$,所以$FE = CE$,所以$FE = AE$,在$Rt\triangle FGE$和$Rt\triangle OHE$中,由“$8$”字型得$\angle FGE=\angle OHE$,又$\angle EFG=\angle AEH = 90^{\circ}$,所以$\triangle EFG\cong\triangle AEH(AAS)$,所以$EG = AH$,因为$EG = BG - BE$,$AH = AC + CH = BD + CH$,所以$BG - BE = BD + CH$,所以$BG = BE + BD + CH = DE + CH$,即$BG = DE + CH$。
③当点$E$在线段$BD$的延长线上时,过点$E$作$EN\perp BA$交$BA$的延长线于点$N$,作$EH'\perp BF$于点$H'$,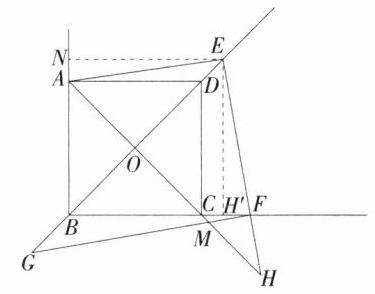
因为$\angle NBE=\angle H'BE = 45^{\circ}$,$\angle NEH'=\angle AEF = 90^{\circ}$,所以$EN = EH'$,$\angle NEH'-\angle AEH'=\angle AEF-\angle AEH'$,即$\angle NEA=\angle H'EF$,因为$\angle ENA=\angle EH'F = 90^{\circ}$,所以$\triangle NEA\cong\triangle H'EF$,所以$AE = EF$,在$Rt\triangle GOM$和$Rt\triangle HFM$中,由“$8$”字型得$\angle G=\angle H$,因为$\angle AEH=\angle EFG = 90^{\circ}$,所以$\triangle AEH\cong\triangle EFG(AAS)$,所以$AH = EG$,因为$AH = AC + CH$,$EG = DE + DB + BG$,$AC = BD$,所以$CH = DE + BG$。
④当点$E$在线段$OB$上时,连接$CE$,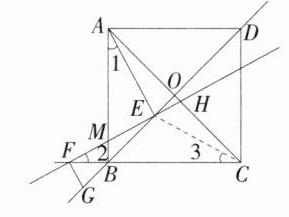
同理得$\angle1=\angle3=\angle2$,$AE = EC = EF$,由“$8$”字型得$\angle EGF=\angle AHE$,因为$\angle EFG=\angle AEH = 90^{\circ}$,所以$\triangle EFG\cong\triangle AEH(AAS)$,所以$EG = AH$,因为$EG = BG + BE = BG + BD - DE$,$AH = AC - CH$,$BD = AC$,所以$BG + BD - DE = AC - CH$,所以$DE = BG + CH$。综上所述,线段$DE$,$BG$,$CH$之间的数量关系为$CH = BG + DE$或$BG = DE + CH$或$DE = BG + CH$。
(1)因为四边形$ABCD$为正方形,$AB=\sqrt{2}$,所以$OA = OB = OD = 1$,$AO\perp BD$,因为点$E$为$OD$的中点,所以$OE=\frac{1}{2}OD=\frac{1}{2}$,所以$BE = BO + OE=\frac{3}{2}$,所以$S_{\triangle ABE}=\frac{1}{2}BE\cdot AO=\frac{1}{2}\times\frac{3}{2}\times1=\frac{3}{4}$。
(2)证明:过点$E$作直线$EN\perp BC$于点$N$,交$AD$于$M$,

易知四边形$AMNB$为矩形,所以$AM = BN$,$\angle AME=\angle AEF=\angle FNE = 90^{\circ}$,在正方形$ABCD$中,$\angle EBN = 45^{\circ}$,所以$EN = BN = AM$,因为$\angle MAE+\angle1=\angle FEN+\angle1 = 90^{\circ}$,所以$\angle MAE=\angle FEN$,所以$\triangle AME\cong\triangle ENF(ASA)$,所以$AE = EF$,同理可得,$\triangle AHE\cong\triangle EGF$,所以$FG = EH$,因为$EH + FH = EF = AE$,所以$FG + FH = AE$。
(3)①当点$E$在线段$OD$上时,由(2)得$\triangle AHE\cong\triangle EGF$,所以$AH = EG$,因为$AH = AC - CH$,$EG = BD - BG - DE$,$AC = BD$,所以$AC - CH = BD - BG - DE$,即$CH = BG + DE$。
②当点$E$在线段$DB$的延长线上时,连接$CE$,

因为四边形$ABCD$是正方形,所以$BD$垂直平分$AC$,$\angle BAO=\angle BCO = 45^{\circ}$,所以$AE = CE$,所以$\angle EAO=\angle ECO$,所以$\angle EAO-\angle BAO=\angle ECO-\angle BCO$,所以$\angle EAB=\angle ECB$,在$Rt\triangle FME$和$Rt\triangle AMB$中,由“$8$”字型得$\angle MAB=\angle MFE$,所以$\angle MFE=\angle ECB$,所以$FE = CE$,所以$FE = AE$,在$Rt\triangle FGE$和$Rt\triangle OHE$中,由“$8$”字型得$\angle FGE=\angle OHE$,又$\angle EFG=\angle AEH = 90^{\circ}$,所以$\triangle EFG\cong\triangle AEH(AAS)$,所以$EG = AH$,因为$EG = BG - BE$,$AH = AC + CH = BD + CH$,所以$BG - BE = BD + CH$,所以$BG = BE + BD + CH = DE + CH$,即$BG = DE + CH$。
③当点$E$在线段$BD$的延长线上时,过点$E$作$EN\perp BA$交$BA$的延长线于点$N$,作$EH'\perp BF$于点$H'$,

因为$\angle NBE=\angle H'BE = 45^{\circ}$,$\angle NEH'=\angle AEF = 90^{\circ}$,所以$EN = EH'$,$\angle NEH'-\angle AEH'=\angle AEF-\angle AEH'$,即$\angle NEA=\angle H'EF$,因为$\angle ENA=\angle EH'F = 90^{\circ}$,所以$\triangle NEA\cong\triangle H'EF$,所以$AE = EF$,在$Rt\triangle GOM$和$Rt\triangle HFM$中,由“$8$”字型得$\angle G=\angle H$,因为$\angle AEH=\angle EFG = 90^{\circ}$,所以$\triangle AEH\cong\triangle EFG(AAS)$,所以$AH = EG$,因为$AH = AC + CH$,$EG = DE + DB + BG$,$AC = BD$,所以$CH = DE + BG$。
④当点$E$在线段$OB$上时,连接$CE$,

同理得$\angle1=\angle3=\angle2$,$AE = EC = EF$,由“$8$”字型得$\angle EGF=\angle AHE$,因为$\angle EFG=\angle AEH = 90^{\circ}$,所以$\triangle EFG\cong\triangle AEH(AAS)$,所以$EG = AH$,因为$EG = BG + BE = BG + BD - DE$,$AH = AC - CH$,$BD = AC$,所以$BG + BD - DE = AC - CH$,所以$DE = BG + CH$。综上所述,线段$DE$,$BG$,$CH$之间的数量关系为$CH = BG + DE$或$BG = DE + CH$或$DE = BG + CH$。
查看更多完整答案,请扫码查看


