《2025年5年中考3年模拟八年级数学下册人教版》

1. [情境题·数学文化]我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国古代的长度单位，则该沙田的面积为(M8217002) ( )
A.78平方里
B.65平方里
C.60平方里
D.30平方里

答案： D 因为 $5^{2}+12^{2}=13^{2}$，所以该三角形沙田是直角三角形，所以沙田的面积 $=\frac{1}{2}×5×12 = 30$（平方里）. 故选D.

2. 为了避免剪刀伤到手，小洛做了一个剪刀套，其示意图如图所示，已知AB = 4，AD = 3，BC = 13，CD = 12，且∠BAD = 90°，连接BD，则∠BDC = ________°.(M8217002)

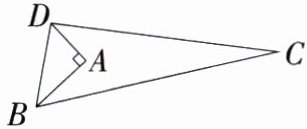
答案： **答案**：90 **解析**：在 $\triangle ABD$ 中，$AB = 4$，$AD = 3$，$\angle BAD = 90^{\circ}$，由勾股定理得 $BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{4^{2}+3^{2}} = 5$，在 $\triangle BCD$ 中，$BC = 13$，$CD = 12$，$BD = 5$，所以 $BC^{2}=BD^{2}+CD^{2}$，所以 $\triangle BCD$ 是直角三角形，且 $\angle BDC = 90^{\circ}$.

3. 为了增强学生的环保意识和生态意识，阳明中学在植树节当天组织了植树活动，这次植树活动中，小洛所在班级一共植树12棵，按如图所示的方式进行分布，已知每相邻的两棵树之间的距离是2 m，则小洛所在班级植树围成的区域(△ABC)的面积为________m².(M8217002)

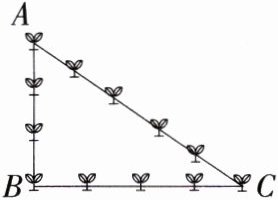
答案： **答案**：24 **解析**：由题意知 $AB = 6\ m$，$BC = 8\ m$，$AC = 10\ m$，所以 $AB^{2}+BC^{2}=AC^{2}$，所以 $\triangle ABC$ 是直角三角形，$\angle ABC = 90^{\circ}$，所以 $S_{\triangle ABC}=\frac{1}{2}×6×8 = 24$（$m^{2}$）.

4. (2024湖北恩施州期末)小明计划制作一架小型飞机模型，如图所示的四边形材料是飞机垂直尾翼，小明测量发现AB = 13 cm，AD = 5 cm，∠DBC = 90°，BC = 16 cm，CD = 20 cm. 根据设计要求需保证AD//BC. 请判断该尾翼是否符合设计要求，并说明理由.(M8217002)

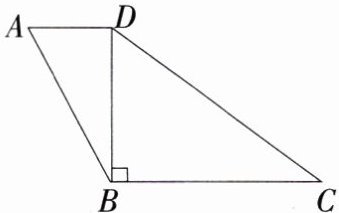
答案： **解析**：符合设计要求. 理由：因为 $\angle DBC = 90^{\circ}$，$BC = 16\ cm$，$CD = 20\ cm$，所以 $BD=\sqrt{CD^{2}-BC^{2}}=\sqrt{20^{2}-16^{2}} = 12$（$cm$），在 $\triangle ABD$ 中，$AB = 13\ cm$，$AD = 5\ cm$，所以 $AD^{2}+BD^{2}=5^{2}+12^{2}=13^{2}=AB^{2}$，所以 $\triangle ABD$ 是直角三角形，且 $\angle ADB = 90^{\circ}$，所以 $\angle ADB=\angle DBC$，所以 $AD// BC$. 故该尾翼符合设计要求.

5. (2021广西玉林中考，16，★★☆)如图，某港口P在东西方向的海岸线上，甲、乙两轮船同时离开港口，各自沿一固定方向航行，甲、乙两轮船每小时分别航行12海里和16海里，1小时后两船分别位于点A、B处，且相距20海里，如果知道甲船沿北偏西40°方向航行，那么乙船沿________方向航行.(M8217002)

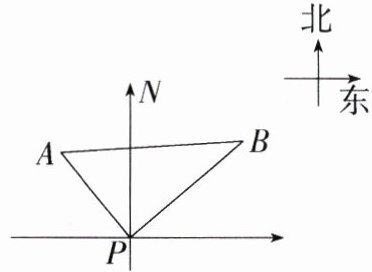
答案： **答案**：北偏东 $50^{\circ}$ **解析**：由题意可知 $AP = 12$ 海里，$BP = 16$ 海里，$AB = 20$ 海里，因为 $12^{2}+16^{2}=20^{2}$，所以 $AP^{2}+BP^{2}=AB^{2}$，所以 $\triangle APB$ 是直角三角形，且 $\angle APB = 90^{\circ}$，由题意知 $\angle APN = 40^{\circ}$，所以 $\angle BPN=\angle APB - \angle APN=90^{\circ}-40^{\circ}=50^{\circ}$，即乙船沿北偏东 $50^{\circ}$ 方向航行.

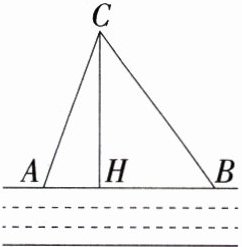
6. (2023山西临汾月考，21，★★☆)如图，在一条东西走向的河的一侧有一村庄C，河边原有两个取水点A，B，其中AB = AC. 由于某种原因，由C到A的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上)，并新修一条公路CH，测得CB = 2千米，CH = 1.6千米，HB = 1.2千米.(M8217002)
(1)公路CH是不是从村庄C到河边的最短路径？请通过计算加以说明.
(2)求原来的路线AC的长.

答案： **解析**： （1）是. 理由：在 $\triangle CHB$ 中，$CB = 2$ 千米，$CH = 1.6$ 千米，$HB = 1.2$ 千米，所以 $CH^{2}+HB^{2}=CB^{2}$，所以 $\triangle CHB$ 是直角三角形，且 $\angle CHB = 90^{\circ}$，所以 $CH\perp AB$，故公路 $CH$ 是从村庄 $C$ 到河边的最短路径. （2）设 $AC = AB = x$ 千米，则 $AH=(x - 1.2)$ 千米，在 $Rt\triangle ACH$ 中，$CH = 1.6$ 千米，由勾股定理得 $AC^{2}=AH^{2}+CH^{2}$，即 $x^{2}=(x - 1.2)^{2}+1.6^{2}$，解得 $x=\frac{5}{3}$. 答：原来的路线 $AC$ 的长为 $\frac{5}{3}$ 千米.