《2025年5年中考3年模拟八年级数学下册人教版》

1.如图,要使平行四边形ABCD成为菱形,需添加的一个条件是(M8218006) ( )

A.AC = AD
B.AB = BC
C.∠ABC = 90°
D.AC = BD

答案： B 因为四边形ABCD是平行四边形，AB = BC，所以平行四边形ABCD是菱形，故选B。

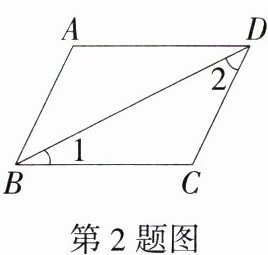
2.如图,在平行四边形ABCD中,∵∠1 = ∠2,∴BC = DC,∴平行四边形ABCD是菱形__________.(请在横线上填上理由)(M8218006)

答案： 有一组邻边相等的平行四边形是菱形。

3.新独家原创 如图所示的是伸缩电动门的一部分,电动门在开、关的过程中,四边形ABCD始终是菱形,则下列结论不正确的是 ( )

A.∠BAD = ∠BCD
B.∠ABC = ∠BCD
C.AB = AD
D.AD = BC

答案： B 因为四边形ABCD是菱形，所以∠BAD = ∠BCD，AB = AD = CD = BC，故选项A、C、D不符合题意，选项B符合题意，故选B。

4.(2023浙江丽水中考)如图,在菱形ABCD中,AB = 1,∠DAB = 60°,则AC的长为 ( )

A.$\frac{1}{2}$
B.1
C.$\frac{\sqrt{3}}{2}$
D.$\sqrt{3}$

答案：
D 如图，连接BD交AC于点O。  因为四边形ABCD是菱形，∠DAB = 60°，所以OA = OC，∠BAO = $\frac{1}{2}$∠DAB = 30°，AC⊥BD，所以∠AOB = 90°，所以OB = $\frac{1}{2}$AB = $\frac{1}{2}$，所以OA = $\sqrt{AB^{2}-OB^{2}}=\sqrt{1^{2}-\left(\frac{1}{2}\right)^{2}}=\frac{\sqrt{3}}{2}$，所以AC = 2OA = $\sqrt{3}$，故选D。

5.情境题·现实生活 图1是伸缩晒衣架,图2是伸缩晒衣架中相邻的三个全等的菱形,根据实际需要可调节A,E间的距离,已知菱形ABCD的边长为20 cm,当A,E间的距离调节到60 cm时,∠DAB的度数是__________.(M8218006)

答案： 答案：120° 解析：连接AE（图略），易知A，C，E三点共线，因为AE = 60 cm，伸缩晒衣架是由三个全等的菱形构成的，所以AC = 20 cm，因为四边形ABCD是菱形，所以BC = AB = 20 cm，所以AC = AB = BC，所以△ABC是等边三角形，所以∠B = 60°，所以∠DAB = 180° - 60° = 120°。

6.(2021贵州黔东南州中考)如图,BD是菱形ABCD的一条对角线,点E在BC的延长线上,若∠ADB = 32°,则∠DCE的度数为__________度.

答案： 答案：64 解析：因为四边形ABCD为菱形，∠ADB = 32°，所以∠CDB = ∠ADB = 32°，AD//BC，所以∠DCE = ∠ADC = ∠ADB + ∠CDB = 64°。

7.(2022辽宁鞍山中考)如图,菱形ABCD的边长为2,∠ABC = 60°,对角线AC与BD交于点O,E为OB中点,F为AD中点,连接EF,则EF的长为__________.(M8218006)

答案：
答案：$\frac{\sqrt{13}}{2}$ 解析：如图，取OD的中点H，连接FH。因为四边形ABCD是菱形，且边长为2，∠ABC = 60°，所以AB = 2，∠ABD = 30°，AC⊥BD，BO = DO，所以AO = $\frac{1}{2}$AB = 1，所以BO = DO = $\sqrt{AB^{2}-AO^{2}}=\sqrt{3}$，因为点H是OD的中点，点F是AD的中点，所以FH = $\frac{1}{2}$AO = $\frac{1}{2}$，FH//AO，所以FH⊥BD，因为点E是BO的中点，点H是OD的中点，所以OE = $\frac{\sqrt{3}}{2}$，OH = $\frac{\sqrt{3}}{2}$，所以EH = $\sqrt{3}$，所以EF = $\sqrt{EH^{2}+FH^{2}}=\sqrt{3 + \frac{1}{4}}=\frac{\sqrt{13}}{2}$。

8.(2024河南安阳期末)已知:如图,在菱形ABCD中,AC为对角线,E是AC上的点,连接BE,DE.
(1)求证:BE = DE.
(2)若BE⊥DE,∠BAD = 60°,AB = 2,求CE的长.

答案：
解析： （1）证明：因为四边形ABCD是菱形，所以CB = CD，∠BCE = ∠DCE，因为CE = CE，所以△BCE≌△DCE（SAS），所以BE = DE。 （2）如图，连接BD交AC于点O。 因为四边形ABCD是菱形，所以AB = AD，AO = OC，OB = OD = $\frac{1}{2}$BD，AC⊥BD，因为∠BAD = 60°，所以△ABD是等边三角形，所以BD = AB = 2，所以OB = OD = 1，所以OC = OA = $\sqrt{AB^{2}-OB^{2}}=\sqrt{3}$，因为BE⊥DE，所以OE = OB = OD = 1，所以CE = OC - OE = $\sqrt{3}-1$。