第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
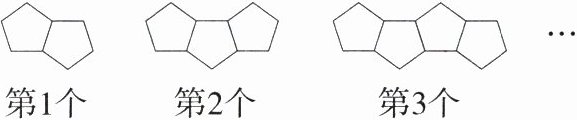
15.新考向·代数推理 如图所示的是用一些木棒拼成的图案,第1个图案用9根木棒拼成,第2个图案用13根木棒拼成,第3个图案用17根木棒拼成,……,按照这个规律,第$n$个图案中木棒的根数是 ( )
A.$4n + 1$
B.$4n - 1$
C.$4n + 5$
D.$5n$

A.$4n + 1$
B.$4n - 1$
C.$4n + 5$
D.$5n$
答案:
C。因为第$1$个图案用$2\times4 + 1 = 9$根木棒拼成,第$2$个图案用$3\times4 + 1 = 13$根木棒拼成,第$3$个图案用$4\times4 + 1 = 17$根木棒拼成,……所以第$n$个图案中木棒的根数是$4(n + 1)+1 = 4n + 5$。故选 C。
20.(2024安徽芜湖月考,17,★★☆)已知$a$满足$\vert2023 - a\vert+\sqrt{a - 2024}=a$.(M8216001)
(1)$\sqrt{a - 2024}$有意义时,$a$的取值范围是________,在这个条件下,将$\vert2023 - a\vert$去掉绝对值符号可得$\vert2023 - a\vert =$________.
(2)根据(1)的分析,求$a - 2023^{2}$的值.
(1)$\sqrt{a - 2024}$有意义时,$a$的取值范围是________,在这个条件下,将$\vert2023 - a\vert$去掉绝对值符号可得$\vert2023 - a\vert =$________.
(2)根据(1)的分析,求$a - 2023^{2}$的值.
答案:
解析:$(1)$因为$\sqrt{a - 2024}$有意义,所以$a - 2024\geq0$,解得$a\geq2024$,所以$\vert2023 - a\vert=a - 2023$,故答案为$a\geq2024$;$a - 2023$。$(2)$由$(1)$得原方程为$a - 2023+\sqrt{a - 2024}=a$,化简得$\sqrt{a - 2024}=2023$,所以$(\sqrt{a - 2024})^{2}=2023^{2}$,所以$a - 2024=2023^{2}$,即$a - 2023^{2}=2024$。
16.(2024河南周口月考,8,★★☆)已知$\triangle ABC$的三边长分别为$a,b,c$,其中$a$和$b$满足$(b - 3)^{2}+\sqrt{a - 5}= 0$,则$c$的取值范围为 ( )
A.$c > 2$
B.$c < 8$
C.$2 < c < 8$
D.$c > 2$或$c < 8$
A.$c > 2$
B.$c < 8$
C.$2 < c < 8$
D.$c > 2$或$c < 8$
答案:
C。因为$(b - 3)^{2}+\sqrt{a - 5}=0$,所以$b - 3 = 0$,$a - 5 = 0$,所以$b = 3$,$a = 5$,因为$a$,$b$,$c$是$\triangle ABC$的三边长,所以$5 - 3\lt c\lt3 + 5$,所以$2\lt c\lt8$,$c$的取值范围为$2\lt c\lt8$。
17.跨物理·人体安全电流 (2024河南郑州四中月考,11,★★☆)一般情况下,人体能够承受的安全电流为0.01 A,电功率$P$(单位:W)与电流$I$(单位:A)、电阻$R$(单位:$\Omega$)之间的公式为$P = I^{2}R$,已知人体电阻阻值约为2 000 $\Omega$,当一充电器电功率为5 W时,若发生触电,则此时通过人体的电流________(填“已”或“未”)超过人体能承受的安全电流.
答案:
答案:已
解析:因为$P = I^{2}R$,所以$I=\sqrt{\frac{P}{R}}$,所以$I=\sqrt{\frac{5}{2000}}=\sqrt{\frac{1}{400}}=\sqrt{(\frac{1}{20})^{2}}=\frac{1}{20}=0.05(A)$。因为$0.05\gt0.01$,所以通过人体的电流已超过人体能承受的安全电流。
18.数形结合思想 (2022四川遂宁中考,12,★★☆)实数$a、b$对应的点在数轴上的位置如图所示,化简:$\vert a + 1\vert-\sqrt{(b - 1)^{2}}+\sqrt{(a - b)^{2}}=$________.
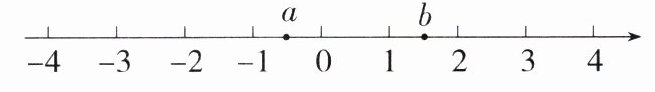
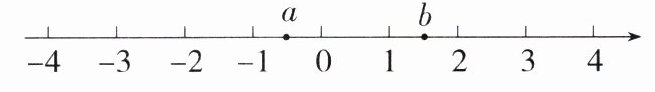
答案:
答案:$2$
解析:由数轴可得$-1\lt a\lt0$,$1\lt b\lt2$,所以$a + 1\gt0$,$b - 1\gt0$,$a - b\lt0$,所以$\vert a + 1\vert-\sqrt{(b - 1)^{2}}+\sqrt{(a - b)^{2}}=a + 1-(b - 1)+(b - a)=a + 1 - b + 1 + b - a = 2$。
19.(2023河北中考,18,★★☆)根据表中的数据,写出$a$的值为________,$b$的值为________.
|结果 代数式|$x$|2|$n$|
|----|----|----|----|
|$3x + 1$| |7|$b$|
|$\frac{2x + 1}{x}$|$a$| |1|
|结果 代数式|$x$|2|$n$|
|----|----|----|----|
|$3x + 1$| |7|$b$|
|$\frac{2x + 1}{x}$|$a$| |1|
答案:
答案:$\frac{5}{2}$;$-2$
解析:当$x = 2$时,$\frac{2x + 1}{x}=\frac{2\times2 + 1}{2}=\frac{5}{2}$,即$a=\frac{5}{2}$。当$x = n$时,$\frac{2n + 1}{n}=1$,解得$n = - 1$,经检验,$n = - 1$是分式方程的解,那么当$x = - 1$时,$3x + 1=-3 + 1=-2$,即$b = - 2$。故答案为$\frac{5}{2}$;$-2$。
21.应用意识 阅读下列解题过程.
例:若代数式$\sqrt{(a - 1)^{2}}+\sqrt{(a - 3)^{2}}$的值是2,求$a$的取值范围.
解:原式$=\vert a - 1\vert+\vert a - 3\vert$,当$a < 1$时,原式$=(1 - a)+(3 - a)= 4 - 2a = 2$,解得$a = 1$(舍去);当$1\leq a\leq3$时,原式$=(a - 1)+(3 - a)= 2$,符合条件;当$a > 3$时,原式$=(a - 1)+(a - 3)= 2a - 4 = 2$,解得$a = 3$(舍去).综上,$a$的取值范围是$1\leq a\leq3$.
上述解题过程主要运用了分类讨论的方法.
请你根据上述材料,解答下列问题:
(1)当$2\leq a\leq3$时,化简:$\sqrt{(a - 2)^{2}}+\sqrt{(a - 5)^{2}}=$________.
(2)若等式$\sqrt{(3 - a)^{2}}+\sqrt{(a - 7)^{2}} = 4$成立,则$a$的取值范围是________.
(3)若$\sqrt{(a + 1)^{2}}+\sqrt{(a - 5)^{2}} = 8$,求$a$的值.
例:若代数式$\sqrt{(a - 1)^{2}}+\sqrt{(a - 3)^{2}}$的值是2,求$a$的取值范围.
解:原式$=\vert a - 1\vert+\vert a - 3\vert$,当$a < 1$时,原式$=(1 - a)+(3 - a)= 4 - 2a = 2$,解得$a = 1$(舍去);当$1\leq a\leq3$时,原式$=(a - 1)+(3 - a)= 2$,符合条件;当$a > 3$时,原式$=(a - 1)+(a - 3)= 2a - 4 = 2$,解得$a = 3$(舍去).综上,$a$的取值范围是$1\leq a\leq3$.
上述解题过程主要运用了分类讨论的方法.
请你根据上述材料,解答下列问题:
(1)当$2\leq a\leq3$时,化简:$\sqrt{(a - 2)^{2}}+\sqrt{(a - 5)^{2}}=$________.
(2)若等式$\sqrt{(3 - a)^{2}}+\sqrt{(a - 7)^{2}} = 4$成立,则$a$的取值范围是________.
(3)若$\sqrt{(a + 1)^{2}}+\sqrt{(a - 5)^{2}} = 8$,求$a$的值.
答案:
解析:$(1)$因为$2\leq a\leq3$,所以$a - 2\geq0$,$a - 5\lt0$,所以原式$=\vert a - 2\vert+\vert a - 5\vert=a - 2-(a - 5)=3$,故答案为$3$。$(2)$由题意可知$\vert3 - a\vert+\vert a - 7\vert = 4$,当$a\leq3$时,$3 - a\geq0$,$a - 7\lt0$,原等式可化为$3 - a-(a - 7)=4$,所以$a = 3$,符合题意;当$3\lt a\lt7$时,$3 - a\lt0$,$a - 7\lt0$,原等式可化为$-(3 - a)-(a - 7)=4$,故$3\lt a\lt7$符合题意;当$a\geq7$时,$3 - a\lt0$,$a - 7\geq0$,原等式可化为$-(3 - a)+(a - 7)=4$,所以$a = 7$,符合题意。综上所述,$3\leq a\leq7$。故答案为$3\leq a\leq7$。$(3)$原方程可化为$\vert a + 1\vert+\vert a - 5\vert = 8$,当$a\leq - 1$时,$a + 1\leq0$,$a - 5\lt0$,原方程可化为$-a - 1-(a - 5)=8$,所以$a = - 2$,符合题意;当$-1\lt a\lt5$时,$a + 1\gt0$,$a - 5\lt0$,原方程可化为$(a + 1)-(a - 5)=8$,此方程无解,故$-1\lt a\lt5$不符合题意;当$a\geq5$时,$a + 1\gt0$,$a - 5\geq0$,原方程可化为$a + 1+a - 5=8$,所以$a = 6$,符合题意。综上所述,$a = - 2$或$a = 6$。
查看更多完整答案,请扫码查看


