《2025年5年中考3年模拟八年级数学下册人教版》

1. 教材变式·P61T12（2023四川自贡中考）如图，边长为3的正方形OBCD的两边落在坐标轴正半轴上，点C的坐标是(M8218007) （ ）
A. (3,-3) B. (-3,3) C. (3,3) D. (-3,-3)

答案： C 因为正方形OBCD的边长为3，所以DC = BC = 3，DC与BC分别垂直于y轴和x轴。又因为点C在第一象限，所以点C的坐标为(3, 3)。

2. 教材变式·P67T1（3） 如图，在正方形ABCD的外侧作等边△ABE，连接ED，则∠BED的度数为(M8218007) （ ）
A. 15° B. 35° C. 45° D. 55°

答案： C 在正方形ABCD中，AB = AD，∠BAD = 90°，在等边△ABE中，AB = AE，∠BAE = ∠AEB = 60°，所以AD = AE，∠DAE = ∠BAD + ∠BAE = 90° + 60° = 150°，则∠AED = ∠ADE = 1/2×(180° - 150°) = 15°，所以∠BED = ∠AEB - ∠AED = 60° - 15° = 45°，故选C。

3. 如图所示的是一块大正方形地板砖，上面的图案是由四个全等的五边形和一个小正方形组成的，若AD = 20 cm，点A是OE的中点，则图中大正方形地板砖的边长为________cm.

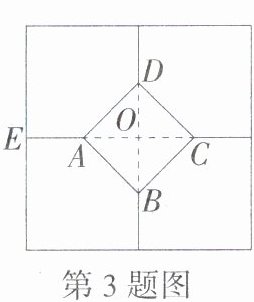
答案： 答案：40√2 解析：因为四边形ABCD是正方形，所以AO = OD，∠AOD = 90°，设AO = OD = x cm，在Rt△AOD中，由勾股定理得AO² + OD² = AD²，即2x² = 400，解得x = 10√2（负值已舍去），因为点A是OE的中点，所以EO = 2AO = 20√2 cm，所以大正方形地板砖的边长为20√2×2 = 40√2 (cm)。

4.（2023山东威海中考）如图，在正方形ABCD中，分别以点A，B为圆心，以AB的长为半径画弧，两弧交于点E，连接DE，则∠CDE = ________°。

答案： 答案：15 解析：由题意知AE = BE = AB，所以△ABE是等边三角形，所以∠EAB = 60°，在正方形ABCD中，AB = AD，∠ADC = ∠DAB = 90°，所以AE = AD，∠DAE = 90° - 60° = 30°，则∠ADE = ∠AED = 1/2×(180° - 30°) = 75°，所以∠CDE = ∠ADC - ∠ADE = 15°。

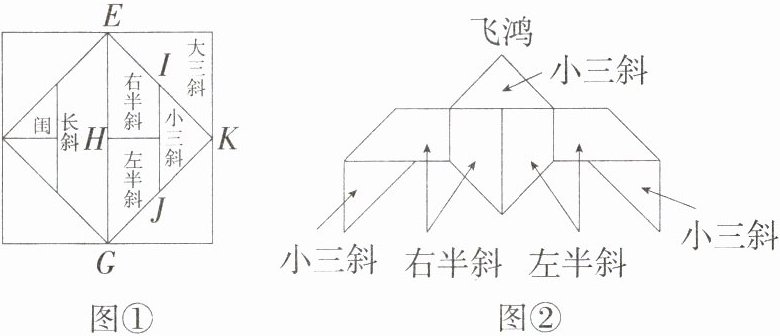
5. 情境题·数学文化 如图①，《蝶几图》是以正方形为模分割为长斜（等腰梯形），右半斜和左半斜（直角梯形），小三斜，大三斜和闺（均为等腰直角三角形），I、J分别为EK、GK的中点. 现取右半斜两张，左半斜两张和小三斜三张，拼成图②所示的“飞鸿”，若图①中大正方形的边长为4，则“飞鸿”的高度为________.（M8218007）

答案：
答案：2 + √2 解析：如图，连接AD，因为题图①中大正方形的边长为4，所以EG = 4，因为I、J分别为EK、GK的中点，所以IJ = 1/2EG = 2，所以BC = IJ = 2，在等腰Rt△IJK中，由勾股定理得IK = √2，所以AB = AC = √2，因为∠BAC = 90°，所以S△ABC = √2×√2×1/2 = 1，因为BC = 2，所以AD = 1，所以BF = BD = AD = 1，因为PQ = AB = √2，所以“飞鸿”的高度为AD + BF + PQ = 1 + 1 + √2 = 2 + √2。

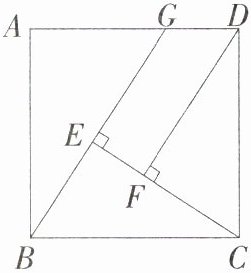
6.（2022湖北恩施州中考）如图，已知四边形ABCD是正方形，G为线段AD上任意一点，CE⊥BG于点E，DF⊥CE于点F. 求证：DF = BE + EF.

答案： 证明：因为四边形ABCD是正方形，所以BC = CD，∠BCD = 90°，因为CE⊥BG，DF⊥CE，所以∠BEC = ∠DFC = 90°，所以∠BCE + ∠CBE = 90° = ∠BCE + ∠DCF，所以∠CBE = ∠DCF，在△CBE和△DCF中，{∠BEC = ∠CFD，∠EBC = ∠FCD，BC = CD}，所以△CBE≌△DCF(AAS)，所以CF = BE，CE = DF，因为CE = CF + EF，所以DF = BE + EF。

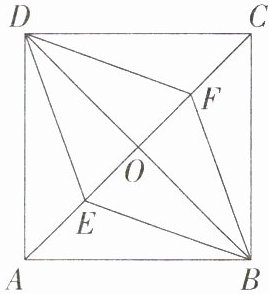
7.（2021湖南邵阳中考）如图，在正方形ABCD中，对角线AC，BD相交于点O，点E，F是对角线AC上的两点，且AE = CF，连接DE，DF，BE，BF.
（1）证明：△ADE≌△CBF.
（2）若AB = 4$\sqrt{2}$，AE = 2，求四边形BEDF的周长.

答案： 解析： （1）证明：因为四边形ABCD是正方形，所以AD = BC，∠DAE = ∠BCF = 45°，在△ADE和△CBF中，{AD = CB，∠DAE = ∠BCF，AE = CF}，所以△ADE≌△CBF(SAS)。 （2）因为四边形ABCD为正方形，所以∠BAD = 90°，AC = BD，OA = OC，OB = OD，AC⊥BD，AD = AB = 4√2，所以BD = √(AB² + AD²) = √((4√2)² + (4√2)²) = 8，所以AC = BD = 8，所以DO = BO = 4，OA = OC = 4，因为AE = CF = 2，所以OA - AE = OC - CF，即OE = OF = 4 - 2 = 2，所以四边形BEDF为平行四边形，因为EF⊥BD，所以四边形BEDF是菱形，因为DE = √(DO² + EO²) = √(4² + 2²) = 2√5，所以四边形BEDF的周长为4DE = 8√5。