第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
4. 如图,在平面直角坐标系中,一次函数 y = 2x - 1 的图象分别交 x 轴、y 轴于点 A、B,将直线 AB 绕点 B 按顺时针方向旋转 45°,交 x 轴于点 C,则直线 BC 的函数表达式是__________.


答案:
**答案**:$y=\frac{1}{3}x-1$ **解析**:因为一次函数$y = 2x-1$的图象分别交$x$轴、$y$轴于点$A$、$B$,所以$A(\frac{1}{2},0)$,$B(0,-1)$,则$OA=\frac{1}{2}$,$OB = 1$。过$A$作$AF\perp AB$交$BC$于$F$,过$F$作$FE\perp x$轴于$E$。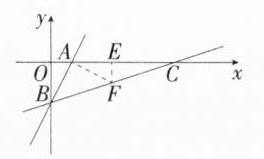
因为$\angle ABC = 45^{\circ}$,所以$\triangle ABF$是等腰直角三角形,所以$AB = AF$。又因为$\angle OAB+\angle ABO=\angle OAB+\angle EAF = 90^{\circ}$,所以$\angle ABO=\angle EAF$,所以$\triangle ABO\cong\triangle FAE(AAS)$,所以$AE = OB = 1$,$EF = OA=\frac{1}{2}$,所以$F(\frac{3}{2},-\frac{1}{2})$。设直线$BC$的函数表达式为$y = kx + b(k\neq0)$,则$\begin{cases}\frac{3}{2}k + b=-\frac{1}{2}\\b=-1\end{cases}$,解得$\begin{cases}k=\frac{1}{3}\\b=-1\end{cases}$,所以直线$BC$的函数表达式为$y=\frac{1}{3}x-1$。
**答案**:$y=\frac{1}{3}x-1$ **解析**:因为一次函数$y = 2x-1$的图象分别交$x$轴、$y$轴于点$A$、$B$,所以$A(\frac{1}{2},0)$,$B(0,-1)$,则$OA=\frac{1}{2}$,$OB = 1$。过$A$作$AF\perp AB$交$BC$于$F$,过$F$作$FE\perp x$轴于$E$。

因为$\angle ABC = 45^{\circ}$,所以$\triangle ABF$是等腰直角三角形,所以$AB = AF$。又因为$\angle OAB+\angle ABO=\angle OAB+\angle EAF = 90^{\circ}$,所以$\angle ABO=\angle EAF$,所以$\triangle ABO\cong\triangle FAE(AAS)$,所以$AE = OB = 1$,$EF = OA=\frac{1}{2}$,所以$F(\frac{3}{2},-\frac{1}{2})$。设直线$BC$的函数表达式为$y = kx + b(k\neq0)$,则$\begin{cases}\frac{3}{2}k + b=-\frac{1}{2}\\b=-1\end{cases}$,解得$\begin{cases}k=\frac{1}{3}\\b=-1\end{cases}$,所以直线$BC$的函数表达式为$y=\frac{1}{3}x-1$。
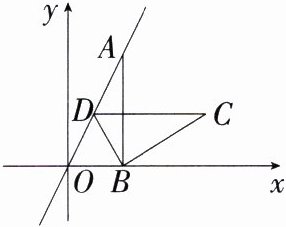
5. 如图,在平面直角坐标系 xOy 中,直线 y = $\sqrt{3}x$经过点 A,作 AB⊥x 轴于点 B,将△ABO 绕点 B 顺时针旋转 60°得到△CBD,若点 B 的坐标为(2,0),则点 C 的坐标为________.

答案:
**答案**:$(5,\sqrt{3})$
**解析**:因为点$B$的坐标为$(2,0)$,所以$OB = 2$,因为$AB\perp x$轴于点$B$,所以点$A$的横坐标为$2$,当$x = 2$时,$y = 2\sqrt{3}$,所以点$A$的坐标为$(2,2\sqrt{3})$,则$AB = 2\sqrt{3}$。由勾股定理得$OA=\sqrt{AB^{2}+OB^{2}}=\sqrt{(2\sqrt{3})^{2}+2^{2}} = 4$,所以$\angle OAB = 30^{\circ}$,$\angle AOB = 60^{\circ}$。因为$\triangle ABO$绕点$B$顺时针旋转$60^{\circ}$得到$\triangle CBD$,所以$\angle C = 30^{\circ}$,$\angle ABC = 60^{\circ}$,设$AB$与$CD$相交于点$E$,所以$\angle BEC = 90^{\circ}=\angle OBA$,所以$CD// x$轴。在$Rt\triangle BEC$中,$BE=\frac{1}{2}BC=\frac{1}{2}AB=\frac{1}{2}\times2\sqrt{3}=\sqrt{3}$,所以$CE=\sqrt{BC^{2}-BE^{2}} = 3$,所以点$C$的横坐标为$3 + 2 = 5$,所以点$C$的坐标为$(5,\sqrt{3})$。
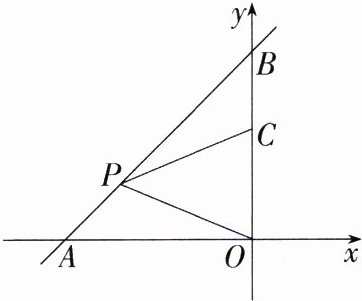
6. (2021 广西贺州中考)如图,一次函数 y = x + 4 的图象与坐标轴分别交于 A,B 两点,点 P,C 分别是线段 AB,OB 上的点,且∠OPC = 45°,PC = PO,则点 P 的坐标为___________.

答案:
**答案**:$(-2\sqrt{2},4 - 2\sqrt{2})$ **解析**:在$y = x + 4$中,令$x = 0$,则$y = 4$;令$y = 0$,则$x=-4$,所以$A(-4,0)$,$B(0,4)$,所以$AO = BO = 4$,所以$\triangle AOB$是等腰直角三角形,$\angle ABO = 45^{\circ}$。过$P$作$PD\perp OC$于$D$,则$\triangle BDP$是等腰直角三角形。
因为$\angle PBC=\angle OPC=\angle OAP = 45^{\circ}$,所以$\angle PCB+\angle BPC = 135^{\circ}=\angle OPA+\angle BPC$,所以$\angle PCB=\angle OPA$。在$\triangle PCB$和$\triangle OPA$中,$\begin{cases}\angle PBC=\angle OAP\\\angle PCB=\angle OPA\\PC = OP\end{cases}$,所以$\triangle PCB\cong\triangle OPA(AAS)$,所以$BP = AO = 4$。在$Rt\triangle BDP$中,$BD = PD = 2\sqrt{2}$,所以$OD = OB - BD=4 - 2\sqrt{2}$,所以点$P$的坐标为$(-2\sqrt{2},4 - 2\sqrt{2})$。
**答案**:$(-2\sqrt{2},4 - 2\sqrt{2})$ **解析**:在$y = x + 4$中,令$x = 0$,则$y = 4$;令$y = 0$,则$x=-4$,所以$A(-4,0)$,$B(0,4)$,所以$AO = BO = 4$,所以$\triangle AOB$是等腰直角三角形,$\angle ABO = 45^{\circ}$。过$P$作$PD\perp OC$于$D$,则$\triangle BDP$是等腰直角三角形。

因为$\angle PBC=\angle OPC=\angle OAP = 45^{\circ}$,所以$\angle PCB+\angle BPC = 135^{\circ}=\angle OPA+\angle BPC$,所以$\angle PCB=\angle OPA$。在$\triangle PCB$和$\triangle OPA$中,$\begin{cases}\angle PBC=\angle OAP\\\angle PCB=\angle OPA\\PC = OP\end{cases}$,所以$\triangle PCB\cong\triangle OPA(AAS)$,所以$BP = AO = 4$。在$Rt\triangle BDP$中,$BD = PD = 2\sqrt{2}$,所以$OD = OB - BD=4 - 2\sqrt{2}$,所以点$P$的坐标为$(-2\sqrt{2},4 - 2\sqrt{2})$。
7. 如图,直线 y = -$\frac{1}{2}x + 3$与坐标轴分别交于点 A,点 B,与直线 y = x 交于点 C,线段 OA 上的点 Q 以每秒 1 个单位长度的速度从点 O 出发向点 A 做匀速运动,运动时间为 t 秒,连接 CQ.
(1)求点 C 的坐标.
(2)若△OQC 是等腰直角三角形,则 t 的值为__________.

(3)若 CQ 平分△OAC 的面积,求直线 CQ 的函数关系式.
(1)求点 C 的坐标.
(2)若△OQC 是等腰直角三角形,则 t 的值为__________.

(3)若 CQ 平分△OAC 的面积,求直线 CQ 的函数关系式.
答案:
**解析**\n(1)联立$\begin{cases}y=-\frac{1}{2}x + 3\\y = x\end{cases}$,解得$\begin{cases}x = 2\\y = 2\end{cases}$,所以点$C$的坐标为$(2,2)$。\n(2)
分情况讨论:如图1,当$\angle CQO = 90^{\circ}$,$CQ = OQ$时,因为$C(2,2)$,所以$OQ = CQ = 2$,所以$t=\frac{2}{1}=2$;如图2,当$\angle OCQ = 90^{\circ}$,$OC = CQ$时,过$C$作$CM\perp OA$于$M$,因为$C(2,2)$,所以$CM = OM = 2$,所以$QM = OM = 2$,所以$OQ = 4$,所以$t=\frac{4}{1}=4$。综上,$t$的值为$2$或$4$。\n(3)令$-\frac{1}{2}x + 3 = 0$,得$x = 6$,所以$A(6,0)$,因为$CQ$平分$\triangle OAC$的面积,所以$Q(3,0)$。设直线$CQ$的函数关系式是$y = kx + b(k\neq0)$,把$C(2,2)$,$Q(3,0)$代入得$\begin{cases}2k + b = 2\\3k + b = 0\end{cases}$,解得$\begin{cases}k=-2\\b = 6\end{cases}$,所以直线$CQ$的函数关系式为$y=-2x + 6$。
**解析**\n(1)联立$\begin{cases}y=-\frac{1}{2}x + 3\\y = x\end{cases}$,解得$\begin{cases}x = 2\\y = 2\end{cases}$,所以点$C$的坐标为$(2,2)$。\n(2)

分情况讨论:如图1,当$\angle CQO = 90^{\circ}$,$CQ = OQ$时,因为$C(2,2)$,所以$OQ = CQ = 2$,所以$t=\frac{2}{1}=2$;如图2,当$\angle OCQ = 90^{\circ}$,$OC = CQ$时,过$C$作$CM\perp OA$于$M$,因为$C(2,2)$,所以$CM = OM = 2$,所以$QM = OM = 2$,所以$OQ = 4$,所以$t=\frac{4}{1}=4$。综上,$t$的值为$2$或$4$。\n(3)令$-\frac{1}{2}x + 3 = 0$,得$x = 6$,所以$A(6,0)$,因为$CQ$平分$\triangle OAC$的面积,所以$Q(3,0)$。设直线$CQ$的函数关系式是$y = kx + b(k\neq0)$,把$C(2,2)$,$Q(3,0)$代入得$\begin{cases}2k + b = 2\\3k + b = 0\end{cases}$,解得$\begin{cases}k=-2\\b = 6\end{cases}$,所以直线$CQ$的函数关系式为$y=-2x + 6$。
8. 如图,直线 $l_{1}$:y = 3x + 3 与 x 轴交于点 A,与 y 轴交于点 B.将线段 AB 先向右平移 7 个单位长度,再向上平移 1 个单位长度,得到线段 CD,连接 AC,BD.
(1)求点 C,D 的坐标.
(2)求四边形 BACD 的面积.
(3)若直线 $l_{2}$:y = ax - 2a + 4 将四边形 BACD 分成面积相等的两部分,请求出 a 的值.

(1)求点 C,D 的坐标.
(2)求四边形 BACD 的面积.
(3)若直线 $l_{2}$:y = ax - 2a + 4 将四边形 BACD 分成面积相等的两部分,请求出 a 的值.

答案:
**解析**\n(1)直线$l_1:y = 3x + 3$与$x$轴交于点$A$,与$y$轴交于点$B$,所以$A(-1,0)$,$B(0,3)$。将线段$AB$先向右平移$7$个单位长度,再向上平移$1$个单位长度,得到线段$CD$,所以$C(6,1)$,$D(7,4)$。\n(2)因为线段$AB$平移得到线段$CD$,所以$AB// CD$,$AB = CD$,所以四边形$BACD$是平行四边形,所以$S_{\square BACD}=2S_{\triangle ABC}$。连接$BC$并延长交$x$轴于点$P$,
因为$B(0,3)$,设直线$BC$的解析式为$y = kx + 3(k\neq0)$,将$C(6,1)$代入得$6k + 3 = 1$,解得$k=-\frac{1}{3}$,所以直线$BC$的解析式为$y=-\frac{1}{3}x + 3$。当$y = 0$时,$0=-\frac{1}{3}x + 3$,解得$x = 9$,所以$P(9,0)$,所以$AP = 9-(-1)=10$,所以$S_{\triangle ABC}=S_{\triangle ABP}-S_{\triangle ACP}=\frac{1}{2}AP\cdot y_{B}-\frac{1}{2}AP\cdot y_{C}=10$,所以$S_{\square BACD}=2S_{\triangle ABC}=20$。\n(3)连接$AD$,$BC$相交于点$E$,
设$AD$所在直线解析式为$y = mx + n(m\neq0)$,将$A(-1,0)$,$D(7,4)$代入$y = mx + n$,得$\begin{cases}-m + n = 0\\7m + n = 4\end{cases}$,解得$\begin{cases}m=\frac{1}{2}\\n=\frac{1}{2}\end{cases}$,所以$y=\frac{1}{2}x+\frac{1}{2}$。联立$\begin{cases}y=-\frac{1}{3}x + 3\\y=\frac{1}{2}x+\frac{1}{2}\end{cases}$,解得$\begin{cases}x = 3\\y = 2\end{cases}$,所以点$E$的坐标为$(3,2)$。易知当直线$l_2$过点$E$时可将四边形$BACD$分成面积相等的两部分,将$E(3,2)$代入直线$l_2:y = ax-2a + 4$,得$3a-2a + 4 = 2$,解得$a=-2$。
**解析**\n(1)直线$l_1:y = 3x + 3$与$x$轴交于点$A$,与$y$轴交于点$B$,所以$A(-1,0)$,$B(0,3)$。将线段$AB$先向右平移$7$个单位长度,再向上平移$1$个单位长度,得到线段$CD$,所以$C(6,1)$,$D(7,4)$。\n(2)因为线段$AB$平移得到线段$CD$,所以$AB// CD$,$AB = CD$,所以四边形$BACD$是平行四边形,所以$S_{\square BACD}=2S_{\triangle ABC}$。连接$BC$并延长交$x$轴于点$P$,

因为$B(0,3)$,设直线$BC$的解析式为$y = kx + 3(k\neq0)$,将$C(6,1)$代入得$6k + 3 = 1$,解得$k=-\frac{1}{3}$,所以直线$BC$的解析式为$y=-\frac{1}{3}x + 3$。当$y = 0$时,$0=-\frac{1}{3}x + 3$,解得$x = 9$,所以$P(9,0)$,所以$AP = 9-(-1)=10$,所以$S_{\triangle ABC}=S_{\triangle ABP}-S_{\triangle ACP}=\frac{1}{2}AP\cdot y_{B}-\frac{1}{2}AP\cdot y_{C}=10$,所以$S_{\square BACD}=2S_{\triangle ABC}=20$。\n(3)连接$AD$,$BC$相交于点$E$,

设$AD$所在直线解析式为$y = mx + n(m\neq0)$,将$A(-1,0)$,$D(7,4)$代入$y = mx + n$,得$\begin{cases}-m + n = 0\\7m + n = 4\end{cases}$,解得$\begin{cases}m=\frac{1}{2}\\n=\frac{1}{2}\end{cases}$,所以$y=\frac{1}{2}x+\frac{1}{2}$。联立$\begin{cases}y=-\frac{1}{3}x + 3\\y=\frac{1}{2}x+\frac{1}{2}\end{cases}$,解得$\begin{cases}x = 3\\y = 2\end{cases}$,所以点$E$的坐标为$(3,2)$。易知当直线$l_2$过点$E$时可将四边形$BACD$分成面积相等的两部分,将$E(3,2)$代入直线$l_2:y = ax-2a + 4$,得$3a-2a + 4 = 2$,解得$a=-2$。
查看更多完整答案,请扫码查看


