《2026年决胜中考数学安徽专版》

1. (2025·安徽池州一模)
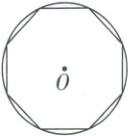
刘徽在《九章算术注》中首创 “割圆术”, 利用圆的内接正多边形来确定圆周率, 开创了中国数学发展史上圆周率研究的新纪元. 某同学在学习 “割圆术” 的过程中, 作了一个如图所示的圆内接正八边形. 若 $ \odot O $ 的半径为 2, 则这个圆内接正八边形的面积为 ()

A.$ 4\sqrt{2} $
B.$ 8\sqrt{2} $
C.$ 4\sqrt{2}\pi $
D.$ 8\sqrt{2}\pi $

答案：
[解析] 如图, 过 $ A $ 作 $ AC \perp OB $ 于 $ C $. $ \because $ 圆的内接正八边形的圆心角为 $ \frac{360^{\circ}}{8} = 45^{\circ} $, $ OA = 2 $, $ \therefore AC = OC = \sqrt{2} $, $ \therefore S_{\triangle OAB} = \frac{1}{2} × 2 × \sqrt{2} = \sqrt{2} $, $ \therefore $ 这个圆的内接正八边形的面积为 $ 8 × \sqrt{2} = 8\sqrt{2} $.
[答案] B

2. (2025·安徽合肥二模)
如图, $ AB $ 是 $ \odot O $ 的直径, $ C $ 是 $ \odot O $ 上一点, 连接 $ AC $, $ OC $, 若 $ AB = 6 $, $ \angle C = 50^{\circ} $, 则 $ \overset{\frown}{BC} $ 的长为 ()


A.$ \frac{4}{3}\pi $
B.$ \frac{5}{3}\pi $
C.$ 2\pi $
D.$ \frac{8}{3}\pi $

答案： [解析] $ \because $ 直径 $ AB = 6 $, $ \therefore $ 半径 $ OB = 3 $. $ \because $ 圆周角 $ \angle C = 50^{\circ} $, $ OA = OC $, $ \therefore \angle A = \angle C = 50^{\circ} $, $ \therefore $ 圆心角 $ \angle BOC = 2\angle C = 100^{\circ} $, $ \therefore \overset{\frown}{BC} $ 的长是 $ \frac{100 × \pi × 3}{180} = \frac{5}{3}\pi $.
[答案] B