第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
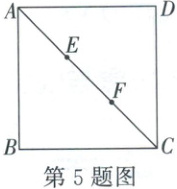
5. (2019·安徽)如图,在正方形$ABCD$中,点$E$,$F$将对角线$AC$三等分,且$AC = 12$,点$P$在正方形的边上,则满足$PE + PF = 9$的点$P$的个数是(
A.$0$
B.$4$
C.$6$
D.$8$
D
)
A.$0$
B.$4$
C.$6$
D.$8$
答案:
5.D [解析]如图,作点$F$关于$BC$的对称点$M$,连接$FM$交$BC$于点$N$,连接$EM$交$BC$于点$H$,连接$CM$,$FH$,则$HF=HM$,$\therefore HE+HF=HE+HM=ME$.$\because$点$E$,$F$将对角线$AC$三等分,且$AC=12$,$\therefore EC=8$,$FC=4=AE$.$\because$点$M$与点$F$关于$BC$对称,$\therefore CF=CM=4$,$\angle ACB=\angle BCM=45^{\circ}$,$\therefore \angle ACM=90^{\circ}$,$\therefore EM=\sqrt{EC^{2}+CM^{2}}=4\sqrt{5}$,即$HE+HF=4\sqrt{5}$,则在线段$BC$上存在点$H$到点$E$和点$F$的距离之和最小,为$4\sqrt{5}$.在点$H$右侧,当点$P$与点$C$重合时,$PE+PF=CE+CF=12$,$\therefore$点$P$在$CH$上时,$4\sqrt{5}\leqslant PE+PF\leqslant12$,$\therefore$在线段$CH$上存在一点$P$,使得$PE+PF=9$.连接$BD$,与$AC$交于点$O$,连接$BE$,$BF$,则$OB=\frac{1}{2}AC=6$,$BD$垂直平分$EF$,$\therefore OE=OF=\frac{1}{2}EF=2$,$\therefore BE=BF=\sqrt{OB^{2}+OF^{2}}=2\sqrt{10}$.在点$H$左侧,当点$P$与点$B$重合时,$PE+PF=BE+BF=4\sqrt{10}$,$\therefore$点$P$在$BH$上时,$4\sqrt{5}\leqslant PE+PF\leqslant4\sqrt{10}$,$\therefore$在线段$BH$上存在一点$P$,使得$PE+PF=9$,$\therefore$在边$BC$上存在$2$个点$P$,满足$PE+PF=9$.同理可得,在边$AB$,$AD$,$CD$上分别存在$2$个满足题意的点$P$.综上所述,满足$PE+PF=9$的点$P$的个数是$2×4=8$.

5.D [解析]如图,作点$F$关于$BC$的对称点$M$,连接$FM$交$BC$于点$N$,连接$EM$交$BC$于点$H$,连接$CM$,$FH$,则$HF=HM$,$\therefore HE+HF=HE+HM=ME$.$\because$点$E$,$F$将对角线$AC$三等分,且$AC=12$,$\therefore EC=8$,$FC=4=AE$.$\because$点$M$与点$F$关于$BC$对称,$\therefore CF=CM=4$,$\angle ACB=\angle BCM=45^{\circ}$,$\therefore \angle ACM=90^{\circ}$,$\therefore EM=\sqrt{EC^{2}+CM^{2}}=4\sqrt{5}$,即$HE+HF=4\sqrt{5}$,则在线段$BC$上存在点$H$到点$E$和点$F$的距离之和最小,为$4\sqrt{5}$.在点$H$右侧,当点$P$与点$C$重合时,$PE+PF=CE+CF=12$,$\therefore$点$P$在$CH$上时,$4\sqrt{5}\leqslant PE+PF\leqslant12$,$\therefore$在线段$CH$上存在一点$P$,使得$PE+PF=9$.连接$BD$,与$AC$交于点$O$,连接$BE$,$BF$,则$OB=\frac{1}{2}AC=6$,$BD$垂直平分$EF$,$\therefore OE=OF=\frac{1}{2}EF=2$,$\therefore BE=BF=\sqrt{OB^{2}+OF^{2}}=2\sqrt{10}$.在点$H$左侧,当点$P$与点$B$重合时,$PE+PF=BE+BF=4\sqrt{10}$,$\therefore$点$P$在$BH$上时,$4\sqrt{5}\leqslant PE+PF\leqslant4\sqrt{10}$,$\therefore$在线段$BH$上存在一点$P$,使得$PE+PF=9$,$\therefore$在边$BC$上存在$2$个点$P$,满足$PE+PF=9$.同理可得,在边$AB$,$AD$,$CD$上分别存在$2$个满足题意的点$P$.综上所述,满足$PE+PF=9$的点$P$的个数是$2×4=8$.

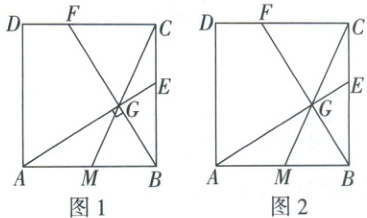
6. (2017·安徽)已知正方形$ABCD$,点$M$为边$AB$的中点。
(1)如图1,点$G$为线段$CM$上的一点,且$\angle AGB = 90^{\circ}$,延长$AG$,$BG$分别与边$BC$,$CD$交于点$E$,$F$。求证:
①$BE = CF$;
②$BE^{2} = BC· CE$;
(2)如图2,在边$BC$上取一点$E$,满足$BE^{2} = BC· CE$,连接$AE$交$CM$于点$G$,连接$BG$延长交$CD$于点$F$,求$\tan\angle CBF$的值。
(1)如图1,点$G$为线段$CM$上的一点,且$\angle AGB = 90^{\circ}$,延长$AG$,$BG$分别与边$BC$,$CD$交于点$E$,$F$。求证:
①$BE = CF$;
②$BE^{2} = BC· CE$;
(2)如图2,在边$BC$上取一点$E$,满足$BE^{2} = BC· CE$,连接$AE$交$CM$于点$G$,连接$BG$延长交$CD$于点$F$,求$\tan\angle CBF$的值。

答案:
6.
(1)证明:①$\because$四边形$ABCD$为正方形,$\therefore AB=BC$,$\angle ABE=\angle BCF=90^{\circ}$.又$\because \angle AGB=90^{\circ}$,$\therefore \angle BAE+\angle ABG=90^{\circ}$.又$\because \angle ABG+\angle CBF=90^{\circ}$,$\therefore \angle BAE=\angle CBF$,$\therefore \triangle ABE\cong\triangle BCF$(ASA),$\therefore BE=CF$.
②$\because \angle AGB=90^{\circ}$,点$M$为$AB$中点,$\therefore MG=MA=MB$,$\therefore \angle GAM=\angle AGM$,$\angle MGB=\angle MBG$.$\because \angle CGE=\angle AGM=\angle GAM$,$\angle GAM+\angle ABG=\angle ABG+\angle CBG=90^{\circ}$,$\therefore \angle CGE=\angle CBG$,$\therefore \triangle CGE\sim\triangle CBG$,$\therefore \frac{CE}{CG}=\frac{CG}{CB}$,即$CG^{2}=BC· CE$.由$\angle CFG=\angle GBM=\angle CGF$,得$CF=CG$.由①知$BE=CF$,$\therefore BE=CG$,$\therefore BE^{2}=BC· CE$.
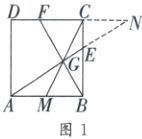
(2)解:方法一:延长$AE$,$DC$交于点$N$(如图1),由于四边形$ABCD$是正方形,$\therefore AB// CD$,$\therefore \angle N=\angle EAB$.又$\angle CEN=\angle BEA$,$\therefore \triangle CEN\sim\triangle BEA$,故$\frac{CE}{BE}=\frac{CN}{BA}$,即$BE· CN=AB· CE$.$\because AB=BC$,$BE^{2}=BC· CE$,$\therefore CN=BE$.由$\begin{cases} AB// DN, \\frac{CN}{AM}=\frac{CG}{GM}=\frac{CF}{MB}. \end{cases}$又$\because AM=MB$,$\therefore FC=CN=BE$,不妨假设正方形边长为1,设$BE=x$,则由$BE^{2}=BC· CE$,得$x^{2}=1·(1 - x)$,解得$x_1=\frac{\sqrt{5}-1}{2}$,$x_2=\frac{-\sqrt{5}-1}{2}$(舍去),$\therefore \frac{BE}{BC}=\frac{\sqrt{5}-1}{2}$,于是$\tan\angle CBF=\frac{FC}{BC}=\frac{BE}{BC}=\frac{\sqrt{5}-1}{2}$.
方法二:不妨假设正方形边长为1,设$BE=x$,则由$BE^{2}=BC· CE$,得$x^{2}=1·(1 - x)$,解得$x_1=\frac{\sqrt{5}-1}{2}$,$x_2=\frac{-\sqrt{5}-1}{2}$(舍去),即$BE=\frac{\sqrt{5}-1}{2}$.作$GN// BC$交$AB$于$N$(如图2),则$\triangle MNG\sim\triangle MBC$,$\therefore \frac{MN}{NG}=\frac{MB}{BC}=\frac{1}{2}$.设$MN=y$,则$GN=2y$,$GM=\sqrt{5}y$.$\because \frac{GN}{BE}=\frac{AN}{AB}$,即$\frac{2y}{\frac{\sqrt{5}-1}{2}}=\frac{y+\frac{1}{2}}{1}$,解得$y=\frac{1}{2\sqrt{5}}$,$\therefore GM=\frac{1}{2}$,从而$GM=MA=MB$,此时点$G$在以$AB$为直径的圆上,$\therefore \triangle AGB$是直角三角形,且$\angle AGB=90^{\circ}$,由
(1)知$BE=CF$,于是$\tan\angle CBF=\frac{FC}{BC}=\frac{BE}{BC}=\frac{\sqrt{5}-1}{2}$.

6.
(1)证明:①$\because$四边形$ABCD$为正方形,$\therefore AB=BC$,$\angle ABE=\angle BCF=90^{\circ}$.又$\because \angle AGB=90^{\circ}$,$\therefore \angle BAE+\angle ABG=90^{\circ}$.又$\because \angle ABG+\angle CBF=90^{\circ}$,$\therefore \angle BAE=\angle CBF$,$\therefore \triangle ABE\cong\triangle BCF$(ASA),$\therefore BE=CF$.
②$\because \angle AGB=90^{\circ}$,点$M$为$AB$中点,$\therefore MG=MA=MB$,$\therefore \angle GAM=\angle AGM$,$\angle MGB=\angle MBG$.$\because \angle CGE=\angle AGM=\angle GAM$,$\angle GAM+\angle ABG=\angle ABG+\angle CBG=90^{\circ}$,$\therefore \angle CGE=\angle CBG$,$\therefore \triangle CGE\sim\triangle CBG$,$\therefore \frac{CE}{CG}=\frac{CG}{CB}$,即$CG^{2}=BC· CE$.由$\angle CFG=\angle GBM=\angle CGF$,得$CF=CG$.由①知$BE=CF$,$\therefore BE=CG$,$\therefore BE^{2}=BC· CE$.
(2)解:方法一:延长$AE$,$DC$交于点$N$(如图1),由于四边形$ABCD$是正方形,$\therefore AB// CD$,$\therefore \angle N=\angle EAB$.又$\angle CEN=\angle BEA$,$\therefore \triangle CEN\sim\triangle BEA$,故$\frac{CE}{BE}=\frac{CN}{BA}$,即$BE· CN=AB· CE$.$\because AB=BC$,$BE^{2}=BC· CE$,$\therefore CN=BE$.由$\begin{cases} AB// DN, \\frac{CN}{AM}=\frac{CG}{GM}=\frac{CF}{MB}. \end{cases}$又$\because AM=MB$,$\therefore FC=CN=BE$,不妨假设正方形边长为1,设$BE=x$,则由$BE^{2}=BC· CE$,得$x^{2}=1·(1 - x)$,解得$x_1=\frac{\sqrt{5}-1}{2}$,$x_2=\frac{-\sqrt{5}-1}{2}$(舍去),$\therefore \frac{BE}{BC}=\frac{\sqrt{5}-1}{2}$,于是$\tan\angle CBF=\frac{FC}{BC}=\frac{BE}{BC}=\frac{\sqrt{5}-1}{2}$.
方法二:不妨假设正方形边长为1,设$BE=x$,则由$BE^{2}=BC· CE$,得$x^{2}=1·(1 - x)$,解得$x_1=\frac{\sqrt{5}-1}{2}$,$x_2=\frac{-\sqrt{5}-1}{2}$(舍去),即$BE=\frac{\sqrt{5}-1}{2}$.作$GN// BC$交$AB$于$N$(如图2),则$\triangle MNG\sim\triangle MBC$,$\therefore \frac{MN}{NG}=\frac{MB}{BC}=\frac{1}{2}$.设$MN=y$,则$GN=2y$,$GM=\sqrt{5}y$.$\because \frac{GN}{BE}=\frac{AN}{AB}$,即$\frac{2y}{\frac{\sqrt{5}-1}{2}}=\frac{y+\frac{1}{2}}{1}$,解得$y=\frac{1}{2\sqrt{5}}$,$\therefore GM=\frac{1}{2}$,从而$GM=MA=MB$,此时点$G$在以$AB$为直径的圆上,$\therefore \triangle AGB$是直角三角形,且$\angle AGB=90^{\circ}$,由
(1)知$BE=CF$,于是$\tan\angle CBF=\frac{FC}{BC}=\frac{BE}{BC}=\frac{\sqrt{5}-1}{2}$.


7. (2025·湖北)如图,折叠正方形$ABCD$的一边$BC$,使点$C$落在$BD$上的点$F$处,折痕$BE$交$AC$于点$G$。若$DE = 2\sqrt{2}$,则$CG$的长是(

A.$\sqrt{2}$
B.$2$
C.$\sqrt{2} + 1$
D.$2\sqrt{2} - 1$
B
)
A.$\sqrt{2}$
B.$2$
C.$\sqrt{2} + 1$
D.$2\sqrt{2} - 1$
答案:
7.B
8. (2025·北京)如图,在正方形$ABCD$中,点$E$在边$CD$上,$CF\perp BE$,垂足为$F$。若$AB = 1$,$\angle EBC = 30^{\circ}$,则$\triangle ABF$的面积为
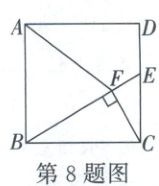
$\frac{3}{8}$
。
答案:
8.$\frac{3}{8}$
9. (2025·乐山)如图,在$□ ABCD$中,对角线$AC$与$BD$相交于点$O$。小乐同学欲添加两个条件使得四边形$ABCD$是正方形,现有三个条件可供选择:①$AC\perp BD$;②$AC = BD$;③$\angle ADC = 90^{\circ}$。则正确的组合是
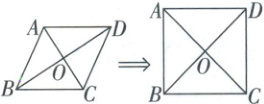
①②(或①③)
(只需填一种组合即可)。
答案:
9.①②(或①③)
10. (2025·威海)把一张矩形纸片按照如图1所示的方式剪成四个全等的直角三角形,四个直角三角形可拼成如图2或图3所示的正方形。若矩形纸片的长为$m$,宽为$n$,四边形$EFGH$的面积等于四边形$ABCD$面积的$2$倍,则$\frac{m}{n}=$

$\frac{2+\sqrt{3}}{2}$
。
答案:
10.$\frac{2+\sqrt{3}}{2}$ [解析]根据题意得,四边形$EFGH$的面积为$m^{2}+(\frac{n}{2})^{2}=m^{2}+\frac{n^{2}}{4}$,四边形$ABCD$的面积为$(m - \frac{n}{2})^{2}=m^{2}-mn+\frac{n^{2}}{4}$.$\because$四边形$EFGH$的面积等于四边形$ABCD$面积的$2$倍,$\therefore m^{2}+\frac{n^{2}}{4}=2(m^{2}-mn+\frac{n^{2}}{4})$,整理得$4m^{2}-8mn + n^{2}=0$,$\therefore 4(\frac{m}{n})^{2}-8·\frac{m}{n}+1=0$.设$\frac{m}{n}=t$,$t>1$,$\therefore 4t^{2}-8t + 1=0$,解得$t=\frac{2+\sqrt{3}}{2}$或$t=\frac{2-\sqrt{3}}{2}$(舍去),$\therefore \frac{m}{n}=\frac{2+\sqrt{3}}{2}$.
查看更多完整答案,请扫码查看


