《2026年决胜中考数学安徽专版》

典例 1
如图，在距某信号塔 $AB$（$AB$ 垂直地面 $BP$）的底部点 $B$ 的右侧 $30m$ 处有一个斜坡，斜坡 $MN$ 的坡度 $i$ 为 $1:2.4$，斜坡上 $4m$ 处有一竖直广告牌 $CD$（即 $MD = 4m$，$CD \perp BP$）。已知当阳光与水平线夹角成 $27^{\circ}$ 时，信号塔的影子顶端正好和广告牌的顶端影子重合于点 $E$（即点 $A$，$C$，$E$ 在同一条直线上），经测量 $DE$ 的长度为 $9m$，求信号塔 $AB$ 的高度。（结果保留整数）
（参考数据：$\sin 27^{\circ} \approx 0.45$，$\tan 27^{\circ} \approx 0.51$）

答案：
解:如图，过点E作EG⊥AB,EF⊥BP，垂足为分别G,F.
　　　　
由题意知,GB=EF,GE=BF,BM=30m.
∵MN的坡度i为1:2.4,
∴EF:MF=1:2.4,
∴设EF=xm,则MF=2.4xm.在Rt△MEF中,ME=MD+DE=4+9=13(m).又
∵EF²+MF²=ME²,
∴x²+(2.4x)²=13²,解得x=5或x=−5(舍去),
∴BG=EF=5m,MF=12m,
∴GE=BF=BM+MF=30+12=42(m).在Rt△AGE中,∠AEG=27°,
∴AG=GE·tan27°=42×0.51=21.42(m),
∴AB=AG+BG=21.42+5≈26(m),
∴信号塔AB的高度约为26m.

典例 2
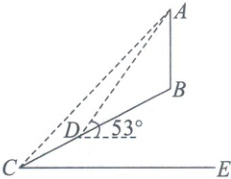
如图，某数学课外实践小组要测斜坡 $CB$ 上基站塔 $AB$ 的高度。已知斜坡 $CB$ 的坡度为 $1:2.4$。在坡脚 $C$ 测得塔顶 $A$ 的仰角为 $45^{\circ}$，再沿坡面 $CB$ 行走了 $13m$ 到达 $D$ 处，在 $D$ 处测得塔顶 $A$ 的仰角为 $53^{\circ}$。（设 $CE$ 为地平线，假定点 $A$，$B$，$C$，$D$ 均在同一平面内）
（1）求 $D$ 处相对于地平线的竖直高度；
（2）求基站塔 $AB$ 的高。
（参考数据：$\sin 53^{\circ}$ 取近似值 $\frac{4}{5}$，$\cos 53^{\circ}$ 取近似值 $\frac{3}{5}$，$\tan 53^{\circ}$ 取近似值 $\frac{4}{3}$）

答案： 解:
(1)如图，过点D作DH⊥CE于点H.
∵DH:CH=1:2.4,设DH=xm,则CH=2.4xm.
∵CD=13,CH²+DH²=CD²,
∴(2.4x)²+x²=13²,解得x=5.
∴D处的竖直高度为5m.
(2)由
(1)得DH=5m,CH=12m.如图,延长AB交CE于点G,则AG⊥CE，作DF⊥AG于点F,
∴∠AFD=∠AGE=90°,GF=DH=5m.在Rt△ACG中,∠ACG=45°,
∴AG=CG.在Rt△ADF中,∠ADF=53°,
∴tan∠ADF=AF/DF=4/3,
∴AF=4/3DF.
∵CH+HG=GF+AF,
∴12+DF=5+4/3DF,解得DF=21，
∴AF=4/3×21=28(m),CG=AG=21+12=33(m).
∵BG:CG=1:2.4,
∴BG=13.75(m),
∴AB=AF+GF−BG=28+5−13.75=19.25(m),
∴基站塔AB的高为19.25m.