《2026年决胜中考数学安徽专版》

1. (2023·安徽)如图，$O$是坐标原点，$Rt\triangle OAB$的直角顶点$A$在$x$轴的正半轴上，$AB = 2$，$\angle AOB = 30^{\circ}$，反比例函数$y = \frac{k}{x}(k ＞ 0)$的图象经过斜边$OB$的中点$C$。
(1)$k =$$\sqrt{3}$；
(2)$D$为该反比例函数图象上的一点，若$DB // AC$，则$OB^2 - BD^2$的值为4。

答案： 1.
(1)$\sqrt{3}$　
(2)4　[解析]
(1)在Rt△OAB 中,AB=2,∠AOB=30°,
∴OB=4,OA=2$\sqrt{3}$,
∴A(2$\sqrt{3}$,0),B(2$\sqrt{3}$,2).
∵C是OB的中点，
∴C($\sqrt{3}$,1).
∵反比例函数y=$\frac{k}{x}$(k＞0)的图象经过点C,
∴1=$\frac{k}{\sqrt{3}}$，解得k=$\sqrt{3}$.
(2)设直线AC的解析式为y=kx+b(k≠0),把(2$\sqrt{3}$,0),($\sqrt{3}$，1)代入，则$\begin{cases}2\sqrt{3}k + b = 0\\\sqrt{3}k + b = 1\end{cases}$，解得$\begin{cases}k = -\frac{\sqrt{3}}{3}\\b = 2\end{cases}$，
∴AC的解析式为y=$-\frac{\sqrt{3}}{3}$x+2。
2.
∵AC//BD,
∴设直线BD的解析式为y=$-\frac{\sqrt{3}}{3}$x+m,把B(2$\sqrt{3}$,2)代入，解得m=4,
∴直线BD的解析式为y=$-\frac{\sqrt{3}}{3}$x+4.
∵点D既在反比例函数图象上，又在直线BD上，
∴联立得$\begin{cases}y = \frac{\sqrt{3}}{x}\\y = -\frac{\sqrt{3}}{3}x + 4\end{cases}$，解得$\begin{cases}x_1 = 2\sqrt{3} + 3\\y_1 = 2 - \sqrt{3}\end{cases}$，$\begin{cases}x_2 = 2\sqrt{3} - 3\\y_2 = 2 + \sqrt{3}\end{cases}$。
当D的坐标为(2$\sqrt{3}$+3,2 - $\sqrt{3}$)时,BD²=(2$\sqrt{3}$+3 - 2$\sqrt{3}$)²+(2 - $\sqrt{3}$ - 2)²=9+3=12,
∴OB² - BD²=16 - 12=4;当D的坐标为(2$\sqrt{3}$ - 3,2 + $\sqrt{3}$)时,BD²=(2$\sqrt{3}$ - 3 - 2$\sqrt{3}$)²+(2 + $\sqrt{3}$ - 2)²=9+3=12,
∴OB² - BD²=16 - 12=4.综上,OB² - BD²=4.

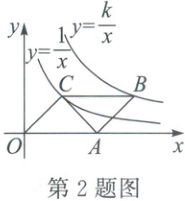
2. (2022·安徽)如图，$□ OABC$的顶点$O$是坐标原点，$A$在$x$轴的正半轴上，$B$，$C$在第一象限，反比例函数$y = \frac{1}{x}$的图象经过点$C$，$y = \frac{k}{x}(k \neq 0)$的图象经过点$B$。若$OC = AC$，则$k =$3。

答案：
2.3 [解析]由题知，反比例函数y=$\frac{1}{x}$的图象经过点C,设C点坐标为(a,$\frac{1}{a}$).作CH⊥OA于点H，过A点作AG⊥BC于点G.
∵四边形OABC是平行四边形,OC=AC,
∴OH=AH,CG=BG,四边形HAGC是矩形，
∴OH=CG=BG=a,即B(3a,$\frac{1}{a}$).
∵y=$\frac{k}{x}$(k≠0)的图象经过点B，
∴k=3a·$\frac{1}{a}$=3.

1. [数学推理]如图，已知点$A(3,3)$，$B(3,1)$，反比例函数$y = \frac{k}{x}(k \neq 0)$图象的一支与线段$AB$有交点，写出一个符合条件的$k$的整数值：k=4(答案不唯一)。
]

答案： 1.k=4(答案不唯一)　[解析]
∵反比例函数y=$\frac{k}{x}$(k＞0)的图象与线段AB 有交点，且点A(3,3),B(3,1),
∴把B(3,1)代入y=$\frac{k}{x}$,得k=3.把A(3,3)代入y=$\frac{k}{x}$,得k=3×3=9,
∴满足条件的k值的范围是3 ≤ k ≤ 9的整数.

2. (2025春·瑶海区校级月考)如图，$\triangle AOB$和$\triangle ACD$都是等腰直角三角形，$\angle ABO = \angle ADC = 90^{\circ}$，点$B$是$y$正半轴上一点，点$C$是反比例函数$y = \frac{16}{x}$的图象上一点，点$D$是$AB$上一点，$OA$与该反比例函数的图象交于点$E$。$\triangle AOB$与$\triangle ACD$的面积之差$S_{\triangle AOB} - S_{\triangle ACD} =$8。
]

答案： 2.8　[解析]设A(m,m),点C(n,$\frac{16}{n}$)，则D(n,m),
∴AD=m - n,CD=$\frac{16}{n}$ - m.
∵AD=CD,
∴m - n=$\frac{16}{n}$ - m,整理得m=$\frac{1}{2}$n+$\frac{8}{n}$，
∴AD=m - n=$\frac{1}{2}$n+$\frac{8}{n}$ - n=$-\frac{1}{2}$n+$\frac{8}{n}$.
∵$S_{\triangle AOB} = \frac{1}{2}AB^2 = \frac{1}{2}m^2 = \frac{1}{2}(\frac{1}{2}n + \frac{8}{n})^2$，$S_{\triangle ACD} = \frac{1}{2}AD^2 = \frac{1}{2}(-\frac{1}{2}n + \frac{8}{n})^2$，
∴$S_{\triangle AOB} - S_{\triangle ACD} = \frac{1}{2}[(\frac{1}{2}n + \frac{8}{n})^2 - (-\frac{1}{2}n + \frac{8}{n})^2] = \frac{1}{2} × (8 + 8) = 8$.

3. （2025·安徽）如图，在平面直角坐标系$xOy$中，一次函数$y = ax + 4(a \neq 0)$与反比例函数$y = \frac{k}{x}(k \neq 0)$的图象交于$A$，$B$两点。已知点$A$和$B$的横坐标分别为$6$和$2$。
(1)求$a$与$k$的值；
(2)设直线$AB$与$x$轴、$y$轴的交点分别为$C$，$D$，求$\triangle COD$的面积。
]

答案： 3.解:
(1)由题意得$\begin{cases}6a + 4 = \frac{k}{6}\\2a + 4 = \frac{k}{2}\end{cases}$，解得$\begin{cases}a = -\frac{1}{2}\\k = 6\end{cases}$
(2)由
(1)知直线AB对应的一次函数表达式为y=$-\frac{1}{2}$x+4,令y=0,得x=8,
∴OC=8.令x=0,得y=4,
∴OD=4,故△COD的面积为$\frac{1}{2}$OC·OD=$\frac{1}{2}$×8×4=16.

4. (2024·安徽)已知反比例函数$y = \frac{k}{x}(k \neq 0)$与一次函数$y = 2 - x$的图象的一个交点的横坐标为$3$，则$k$的值为(A)

A.$-3$
B.$-1$
C.$1$
D.$3$

答案： 4.A　[解析]将x=3代入y=2 - x中,得y= -1,将(3, -1)代入y=$\frac{k}{x}$中，得k= -3.

5. （2021·安徽）已知正比例函数$y = kx(k \neq 0)$与反比例函数$y = \frac{6}{x}$的图象都经过点$A(m,2)$。
(1)求$k$，$m$的值；
(2)在图中画出正比例函数$y = kx$的图象，并根据图象，写出正比例函数值大于反比例函数值时$x$的取值范围。
]

答案：
5.解:
(1)将点A坐标代入反比例函数，得2m=6,
∴m=3,
∴A(3,2).将点A坐标代入正比例函数，得2=3k，
∴k=$\frac{2}{3}$.
(2)如图所示

∴正比例函数值大于反比例函数值时x 的取值范围为x＞3或 -3＜x＜0.