第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
1.(2024·安徽)如图,在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,$AB = 4$,$BC = 2$,$BD$是边$AC$上的高.点$E$,$F$分别在边$AB$,$BC$上(不与端点重合),且$DE \perp DF$.设$AE = x$,四边形$DEBF$的面积为$y$,则$y$关于$x$的函数图象为 ()
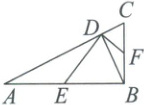



答案:
1.A [解析]如图,过点D作$DH\perp AB$于点H.
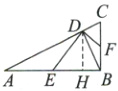
$\because\angle ABC=90^{\circ},AB=4,BC=2,\therefore AC=$
$\sqrt{AB^{2}+BC^{2}}=2\sqrt{5}.\because BD$是边AC上的高,$\therefore BD=\frac{AB· BC}{AC}=\frac{4×2}{2\sqrt{5}}=\frac{4\sqrt{5}}{5}$,
$\therefore CD=\sqrt{BC^{2}-BD^{2}}=\frac{2\sqrt{5}}{5},AD=AC - CD=\frac{8\sqrt{5}}{5}$.
$\because$在$\triangle ABD$中,$DH$是边$AB$上的高,$\therefore DH=\frac{AD· BD}{AB}=\frac{\frac{8\sqrt{5}}{5}×\frac{4\sqrt{5}}{5}}{4}=\frac{8}{5}$.
设$AE=x$,$0<x<4$,$\therefore S_{\triangle ADE}=\frac{1}{2}AE· DH=\frac{1}{2}×\frac{8}{5}× x=\frac{4}{5}x$,
$S_{\triangle BDE}=\frac{1}{2}BE· DH=\frac{1}{2}(4 - x)×\frac{8}{5}=\frac{16}{5}-\frac{4}{5}x$.
$\because\angle BDE=90^{\circ}-\angle BDF=\angle CDF$,$\angle DBE=90^{\circ}-\angle CBD=\angle C$,$\therefore\triangle BDE\sim\triangle CDF$,
$\therefore\frac{S_{\triangle CDF}}{S_{\triangle BDE}}=(\frac{CD}{BD})^{2}=(\frac{\frac{2\sqrt{5}}{5}}{\frac{4\sqrt{5}}{5}})^{2}=\frac{1}{4}$
$\therefore S_{\triangle CDF}=\frac{1}{4}S_{\triangle BDE}=\frac{1}{4}(\frac{16}{5}-\frac{4}{5}x)$.
$\therefore y=S_{\triangle ABC}-S_{\triangle ADE}-S_{\triangle CDF}=\frac{1}{2}×2×4-\frac{4}{5}x-(\frac{4}{5}-\frac{1}{5}x)=-\frac{3}{5}x+\frac{16}{5}(0<x<4).$
$\because-\frac{3}{5}<0$,$\therefore$当$0<x<4$时,$y$随$x$的增大而减小,且$y$与$x$的函数图象为线段(不含端点),观察各选项图象可知,A符合题意.
1.A [解析]如图,过点D作$DH\perp AB$于点H.

$\because\angle ABC=90^{\circ},AB=4,BC=2,\therefore AC=$
$\sqrt{AB^{2}+BC^{2}}=2\sqrt{5}.\because BD$是边AC上的高,$\therefore BD=\frac{AB· BC}{AC}=\frac{4×2}{2\sqrt{5}}=\frac{4\sqrt{5}}{5}$,
$\therefore CD=\sqrt{BC^{2}-BD^{2}}=\frac{2\sqrt{5}}{5},AD=AC - CD=\frac{8\sqrt{5}}{5}$.
$\because$在$\triangle ABD$中,$DH$是边$AB$上的高,$\therefore DH=\frac{AD· BD}{AB}=\frac{\frac{8\sqrt{5}}{5}×\frac{4\sqrt{5}}{5}}{4}=\frac{8}{5}$.
设$AE=x$,$0<x<4$,$\therefore S_{\triangle ADE}=\frac{1}{2}AE· DH=\frac{1}{2}×\frac{8}{5}× x=\frac{4}{5}x$,
$S_{\triangle BDE}=\frac{1}{2}BE· DH=\frac{1}{2}(4 - x)×\frac{8}{5}=\frac{16}{5}-\frac{4}{5}x$.
$\because\angle BDE=90^{\circ}-\angle BDF=\angle CDF$,$\angle DBE=90^{\circ}-\angle CBD=\angle C$,$\therefore\triangle BDE\sim\triangle CDF$,
$\therefore\frac{S_{\triangle CDF}}{S_{\triangle BDE}}=(\frac{CD}{BD})^{2}=(\frac{\frac{2\sqrt{5}}{5}}{\frac{4\sqrt{5}}{5}})^{2}=\frac{1}{4}$
$\therefore S_{\triangle CDF}=\frac{1}{4}S_{\triangle BDE}=\frac{1}{4}(\frac{16}{5}-\frac{4}{5}x)$.
$\therefore y=S_{\triangle ABC}-S_{\triangle ADE}-S_{\triangle CDF}=\frac{1}{2}×2×4-\frac{4}{5}x-(\frac{4}{5}-\frac{1}{5}x)=-\frac{3}{5}x+\frac{16}{5}(0<x<4).$
$\because-\frac{3}{5}<0$,$\therefore$当$0<x<4$时,$y$随$x$的增大而减小,且$y$与$x$的函数图象为线段(不含端点),观察各选项图象可知,A符合题意.
2.(2016·安徽)一段笔直的公路$AC$长$20\ km$,途中有一处休息点$B$,$AB$长$15\ km$,甲、乙两名长跑爱好者同时从点$A$出发,甲以$15\ km/h$的速度匀速跑至点$B$,原地休息半小时后,再以$10\ km/h$的速度匀速跑至终点$C$;乙以$12\ km/h$的速度匀速跑至终点$C$.下列选项中,能正确反映甲、乙两人出发后$2\ h$内运动路程$y(km)$与时间$x(h)$函数关系的图象是 ()


答案:
2.A [解析]甲的运动状态分三种情况:①从点A到点B,速度是15km/h,路程是15km,所用时间为1h,函数的图象是一条线段,两个端点坐标为$(0,0)$和$(1,15)$.②在点B处休息半小时,函数图象是平行于x轴的线段,另一个端点的坐标是$(\frac{3}{2},15)$.③从点B到终点,图象也是一条线段,端点坐标为$(\frac{3}{2},15)$和$(2,20)$.反映乙的运动的函数图象是一条线段,端点坐标为$(0,0),(\frac{5}{3},20)$.符合题意的只有A.
3.(2022·安徽)甲、乙、丙、丁四个人步行的路程和所用的时间如图所示,按平均速度计算,走得最快的是 ()
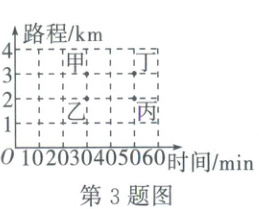
A.甲
B.乙
C.丙
D.丁

A.甲
B.乙
C.丙
D.丁
答案:
3.A [解析]$\because30$min甲比乙步行的路程多,$50$min内丁比丙步行的路程多,$\therefore$甲的平均速度$>$乙的平均速度,丁的平均速度$>$丙的平均速度.$\because$步行$3$km时,甲比丁用的时间少,$\therefore$甲的平均速度$>$丁的平均速度,$\therefore$走得最快的是甲.
4.(2025·乐山)如图,在平面直角坐标系中,点$P$的坐标是 ()

A.$(-3,-2)$
B.$(-3,2)$
C.$(3,2)$
D.$(3,-2)$

A.$(-3,-2)$
B.$(-3,2)$
C.$(3,2)$
D.$(3,-2)$
答案:
4.C
5.(2025·内江)在函数$y = \sqrt{x - 2}$中,自变量$x$的取值范围是 ()
A.$x \geq 2$
B.$x \leq 2$
C.$x > 2$
D.$x < 2$
A.$x \geq 2$
B.$x \leq 2$
C.$x > 2$
D.$x < 2$
答案:
5.A
6.(2025·云南)函数$y = \frac{1}{x - 1}$的自变量$x$的取值范围为 ()
A.$x \neq 4$
B.$x \neq 3$
C.$x \neq 2$
D.$x \neq 1$
A.$x \neq 4$
B.$x \neq 3$
C.$x \neq 2$
D.$x \neq 1$
答案:
6.D
7.(2025·贵州)如图,用一根管子向图中容器注水,若单位时间内注水量保持不变,则从开始到注满容器的过程中,容器内水面升高的速度 ()

A.越来越慢
B.越来越快
C.保持不变
D.快慢交替变化

A.越来越慢
B.越来越快
C.保持不变
D.快慢交替变化
答案:
7.B
查看更多完整答案,请扫码查看


