《2026年决胜中考数学安徽专版》

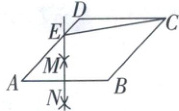
1. (2025·池州二模)如图，在菱形ABCD中，∠A=45°，分别以点A和B为圆心，以大于$\frac{1}{2}$AB的长为半径作弧，两弧相交于点M和N，作直线MN，交AD于点E，连接CE，若AB=2，则CE的长为 (A)

A.$\sqrt{6}$
B.$\sqrt{2}+1$
C.$\sqrt{3}+1$
D.$2\sqrt{2}$

答案：
1.A[解析]如图，连接BE，设直线MN交AB于点F.
∵四边形ABCD为菱形,
∴BC=AB=2,∠ABC=180°−∠A=135°.由作图知，直线MN为线段AB的垂直平分线，
∴AE=BE,∠AFE=90°,AF=$\frac{1}{2}$AB=1.
∵∠A=45°,
∴∠ABE=∠A=45°,AE=$\sqrt{2}$AF=$\sqrt{2}$=BE,
∴∠EBC=∠ABC−∠ABE=90°,
∴在Rt△BCE中，由勾股定理得CE=$\sqrt{BC^2 + BE^2} = \sqrt{2^2 + (\sqrt{2})^2} = \sqrt{6}$.
　　　　　　　　　　

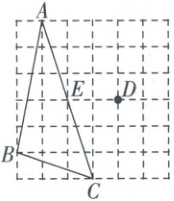
2. (2025·合肥校级四模)如图，在平面直角坐标系中，正方形网格中的每个小正方形边长均为1个单位长度.已知A(-1，-3)，B(-3，2)，连接AB，根据条件画图.
(1)画出线段AB关于y轴对称的线段A₁B₁；
(2)将线段A₁B₁绕着点A₁逆时针旋转90°，得到线段A₁C，则△ABC的面积是$\frac{11}{2}$；
(3)在x轴上取一点P使PC+PB₁的值最小，请直接写出点P的坐标.

答案：
2.解:
(1)如图，A1B1即为所求.
　　　　　
(2)$\frac{11}{2}$　[解析]如图，A1C即为所求.
　　　　　
∵B(−3,2),A(−1,−3),
∴B1(3,2),A1(1,−3).
∵线段A1B1绕着点A1逆时针旋转90°,得到线段A1C,
∴C(−4,−1),
∴S△ABC=5×3−$\frac{1}{2}$×1×3−$\frac{1}{2}$×2×3−$\frac{1}{2}$×2×5=$\frac{11}{2}$.
(3)如图,连接B1C交x轴于点P,根据两点之间，线段最短可得点P即为所求,点P的坐标为(−$\frac{5}{3}$,0).
[解析]设直线B1C的解析式为y=kx+b,把B1(3,2),C(−4,−1)代入得$\begin{cases} 2 = 3k + b \\ -1 = -4k + b \end{cases}$，解得$\begin{cases} k = \frac{3}{7} \\ b = \frac{5}{7} \end{cases}$，所以直线B1C的解析式为y=$\frac{3}{7}$x+$\frac{5}{7}$,令y=0,得0=$\frac{3}{7}$x+$\frac{5}{7}$，解得x=−$\frac{5}{3}$,
∴P(−$\frac{5}{3}$,0).
　　　　　

3. (2025·定远县三模)如图，在由边长为1个单位长度的小正方形组成的网格中，相交于点O的两条线段AB，CD的端点均为格点(网格线的交点).
(1)将线段AB先向左平移2个单位长度，再向上平移4个单位长度，得到线段A₁B₁，画出线段A₁B₁；
(2)画出线段AB关于直线CD对称的线段A₂B₂；
(3)描出线段A₁B₁上的点P，使得点P在∠BOB₂的平分线上，此时$\frac{PB_1}{PA_1}$的值为.

答案： 3.解:
(1)如图，线段A1B1即为所求.
(2)如图，线段A2B2即为所求.
(3)如图，点P即为所求.

4. (2025·庐阳区模拟)将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，其中FM，GN是折痕，若正方形EFGH与五边形MCNGF面积相等.
(1)∠NGF=135°；
(2)$\frac{FM}{GF}$的值是$\frac{\sqrt{5} - \sqrt{2}}{2}$.

答案：
4.解:
(1)135　
(2)$\frac{\sqrt{5} - \sqrt{2}}{2}$
[解析]
(1)连接HF，设直线MH与AD边的交点为P，如图所示.由折叠可知点P,H,F,M四点共线，且PH=MF,∠NGF=∠NGH=$\frac{1}{2}$×(360°−90°)=135°.
(2)设正方形ABCD的边长为2a，则正方形ABCD的面积为4a².
∵正方形EFGH与五边形MCNGF的面积相等，
∴由折叠可知正方形EFGH的面积=$\frac{1}{5}$×正方形ABCD的面积=$\frac{4}{5}$a²,
∴正方形EFGH的边长GF=$\frac{2\sqrt{5}}{5}$a,
∴HF=$\sqrt{2}$GF=$\frac{2\sqrt{10}}{5}$a,
∴MF=PH=$\frac{2a - \frac{2\sqrt{10}}{5}a}{2} = \frac{5 - \sqrt{10}}{5}a$,$\frac{FM}{GF} = \frac{\frac{5 - \sqrt{10}}{5}a}{\frac{2\sqrt{5}}{5}a} = \frac{\sqrt{5} - \sqrt{2}}{2}$.
　　　　　　　　　　　　

5. (2025·宁夏)如图，在6×6的方格中，每个小正方形边长均为1个单位长度.△ABC的顶点、点D和点E都在格点上.仅用无刻度直尺作图，保留作图痕迹，不写作法.
(1)过点D作BC的垂线段；
(2)过点E作BC的平行线.

答案：
5.解:
(1)如图，线段CD即为所求.
(2)如图，直线ET即为所求.

6. 如图是由边长为1的小菱形构成的网格，每个小菱形的顶点称为格点.点A，B均在格点上，请仅用无刻度的直尺作图.
(1)在图1中画出一个以AB为边的菱形ABCD，使点C，D在格点上；
(2)在图2中画出一个以AB为对角线的矩形AEBF，使点E，F在格点上.

答案：
6.解:
(1)如图1，菱形ABCD即为所求.
(2)如图2,矩形AEBF即为所求.