《2026年决胜中考数学安徽专版》

2. (2025·安徽)下列方程中，有两个不相等的实数根的是()

A.$x^{2}+1 = 0$
B.$x^{2}-2x + 1 = 0$
C.$x^{2}+x + 1 = 0$
D.$x^{2}+x - 1 = 0$

答案： 2.D

3. (2022·安徽)若一元二次方程$2x^{2}-4x + m = 0$有两个相等的实数根，则$m=$

答案： 3.2

4. (2018·安徽)若关于$x$的一元二次方程$x(x + 1)+ax = 0$有两个相等的实数根，则实数$a$的值为()

A.$-1$
B.$1$
C.$-2$或$2$
D.$-3$或$1$

答案： 4.A [解析]原方程整理为$x^2 + (a + 1)x = 0$,Δ=$(a + 1)^2 - 4 × 1 × 0 = (a + 1)^2$,由一元二次方程有两个相等的实数根,得Δ=0,即$(a + 1)^2 = 0$,解得$a_1 = a_2 = -1$.

(2025·宁国市一模)若关于$x$的一元二次方程$x^{2}+bx + c = 0$有两个相等的实数根，则$2b^{2}-8c + 1$的值为

答案： 【变式训练】 1[解析]
∵一元二次方程$x^2 + bx + c = 0$有两个相等的实数根,
∴Δ=$b^2 - 4c = 0$,
∴$2b^2 - 8c = 2(b^2 - 4c) = 0$,
∴$2b^2 - 8c + 1 = 1$.

5. (2017·安徽)一种药品原价每盒$25$元，经过两次降价后每盒$16$元。设两次降价的百分率都为$x$，则$x$满足()

A.$16(1 + 2x)=25$
B.$25(1 - 2x)=16$
C.$16(1 + x)^{2}=25$
D.$25(1 - x)^{2}=16$

答案： 5.D [解析]第一次降价后的价格为$25 × (1 - x)$;第二次降价后的价格为$25 × (1 - x)^2$.
∵两次降价后的价格为16元,
∴$25(1 - x)^2 = 16$.

1. (2025·舒城县模拟)近年来我国新能源汽车发展迅速，据中国汽车乘联会统计，$2022$年我国新能源汽车销售量约为$650$万辆，$2024$年约为$1150$万辆，假设我国新能源汽车销售增长率保持不变，预计我国新能源汽车销售量突破$2000$万辆的年份是()
A.$2025$年
B.$2026$年
C.$2027$年
D.$2028$年

答案： 【变式训练】 1.B [解析]设2022年至2024年我国新能源汽车销售增长率为$x$,则2023年我国新能源汽车销售量约为$650(1 + x)$万辆,2024年我国新能源汽车销售量约为$650(1 + x)^2$万辆.由题知$650(1 + x)^2 = 1150$,解得$x_1 ≈ 0.33 = 33\%$,$x_2 ≈ -2.33$(不合题意,舍去),即2022年至2024年我国新能源汽车销售增长率约为33%,
∴$1150(1 + x) ≈ 1150 × (1 + 33\%) = 1529.5$,$1150 × (1 + x)^2 ≈ 1150 × (1 + 33\%)^2 = 2034.235$,即预计我国新能源汽车销售量突破2000万辆的年份是2026年.

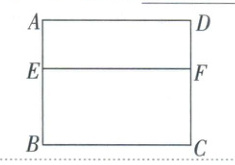
2. 在$20$世纪$70$年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果。如图，利用黄金分割法，所作$EF$将矩形窗框$ABCD$分为上下两部分，其中$E$为边$AB$的黄金分割点，即$BE^{2}=AE· AB$。已知$AB$为$2$米，则线段$BE$的长为米

答案：  2.$-1 + \sqrt{5}$ [解析]设$BE = x$米.则$AE = (2 - x)$米.
∵$BE^2 = AE · AB$.
∴$x^2 = 2(2 - x)$,即$x^2 + 2x - 4 = 0$.解得$x = -1 + \sqrt{5}$,$x_2 = -1 - \sqrt{5}$(舍去),
∴线段BE的长为$(-1 + \sqrt{5})$米.

6. (2025·达州)已知关于$x$的方程$x^{2}+mx - 3 = 0$的一个根是$1$，则$m$的值为

答案： 6.2

7. (2025·上海)已知关于$x$的一元二次方程$2x^{2}+x - m = 0$没有实数根，$m$的取值范围是

答案： 7.$m ＜ -\frac{1}{8}$

8. (2025·泸州)若一元二次方程$2x^{2}-6x - 1 = 0$的两根为$\alpha$，$\beta$，则$2\alpha^{2}-3\alpha+\beta$的值为

答案： 8.10

9. （2025·南充）设$x_{1}$，$x_{2}$是关于$x$的方程$(x - 1)(x - 2)=m^{2}$的两根
（1）当$x_{1}=-1$时，求$x_{2}$及$m$的值；
（2）求证：$(x_{1}-1)(x_{2}-1)\leq0$

答案： 9.
(1)解:把$x_1 = -1$代入方程$(x - 1)(x - 2) = m^2$,得$m^2 = 6$,
∴$m = \pm \sqrt{6}$.
∴$(x - 1)(x - 2) = 6$,即$x^2 - 3x - 4 = 0$.
∴$(x - 4)(x + 1) = 0$.
∴$x_1 = -1$,$x_2 = 4$.
∴$x_2 = 4$,$m = \pm \sqrt{6}$.
(2)证明:方程$(x - 1)(x - 2) = m^2$可化为$x^2 - 3x + 2 - m^2 = 0$.
∵Δ=$4m^2 + 1 ＞ 0$,
∴原方程有两个不相等的实数根,由根与系数的关系得$x_1 + x_2 = 3$,$x_1x_2 = 2 - m^2$,
∴$(x_1 - 1)(x_2 - 1) = x_1x_2 - (x_1 + x_2) + 1 = 2 - m^2 - 3 + 1 = -m^2$.
∵$-m^2 ≤ 0$,
∴$(x_1 - 1)(x_2 - 1) ≤ 0$.

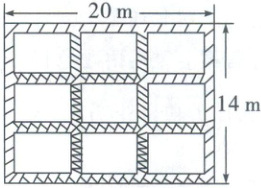
10. （2025·威海）如图，某校有一块长$20\space m$、宽$14\space m$的矩形种植园。为了方便耕作管理，在种植园的四周和内部修建宽度相同的小路（图中阴影部分）小路把种植园分成面积均为$24\space m^{2}$的$9$个矩形地块，请你求出小路的宽度

答案： 10.解:设小路的宽度为$x$米.由题意得,$(20 - 4x)(14 - 4x) = 24 × 9$,整理得$2x^2 - 17x + 8 = 0$,解得$x = 0.5$或$x = 8$(舍去).答:小路的宽度为0.5米.