第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
典例1(2025·安徽模拟预测)
如图,直线$l$与正五边形$ABCDE$的边$AB$,$CD$分别相交于点$F$,$G$,则$\alpha+\beta$的大小为()

A.$120^{\circ}$
B.$136^{\circ}$
C.$144^{\circ}$
D.$150^{\circ}$
如图,直线$l$与正五边形$ABCDE$的边$AB$,$CD$分别相交于点$F$,$G$,则$\alpha+\beta$的大小为()

A.$120^{\circ}$
B.$136^{\circ}$
C.$144^{\circ}$
D.$150^{\circ}$
答案:
[解析] $\because ABCDE$为正五边形,$\therefore\angle B=\angle C=\frac{(5 - 2)×180^{\circ}}{5}=108^{\circ}$,$\therefore\angle GFB+\angle FGC = 360^{\circ}-\angle B-\angle C = 144^{\circ}$。$\because\alpha=\angle GFB$,$\beta=\angle FGC$,$\therefore\alpha+\beta = 144^{\circ}$。
[答案] C
[答案] C
典例2(2025·新疆)
如图,在$□ ABCD$中,$\angle BCD$的平分线交$AB$于点$E$,若$AD = 2$,则$BE=$。

如图,在$□ ABCD$中,$\angle BCD$的平分线交$AB$于点$E$,若$AD = 2$,则$BE=$。

答案:
[解析] $\because$四边形$ABCD$是平行四边形,$AD = 2$,$\therefore AB// CD$,$AD = BC = 2$,$\therefore\angle DCE=\angle CEB$。$\because\angle BCD$的平分线交$AB$于点$E$,$\therefore\angle DCE=\angle BCE$,$\therefore\angle BCE=\angle BEC$,$\therefore BE = BC = 2$。
[答案] $2$
[答案] $2$
1.(2015·安徽)如图所示,在四边形$ABCD$中,$\angle A=\angle B=\angle C$,点$E$在边$AB$上,$\angle AED = 60^{\circ}$,则一定有(
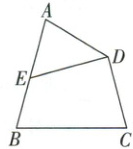
A.$\angle ADE = 20^{\circ}$
B.$\angle ADE = 30^{\circ}$
C.$\angle ADE=\frac{1}{2}\angle ADC$
D.$\angle ADE=\frac{1}{3}\angle ADC$
D
)
A.$\angle ADE = 20^{\circ}$
B.$\angle ADE = 30^{\circ}$
C.$\angle ADE=\frac{1}{2}\angle ADC$
D.$\angle ADE=\frac{1}{3}\angle ADC$
答案:
1.D [解析]设$\angle ADE = x^{\circ},\angle ADC = y^{\circ}$,由题意可得,$\angle ADE+\angle AED+\angle A = 180^{\circ}$,$\angle A+\angle B+\angle C+\angle ADC = 360^{\circ}$,即$x + 60 + \angle A = 180·s①$,$3\angle A + y = 360·s②$,由①×3 - ②可得$3x - y = 0$,$\therefore x=\frac{1}{3}y$,即$\angle ADE=\frac{1}{3}\angle ADC$。
(2025·湖北模拟预测)如图,将正五边形剪掉一个角(裁剪线不经过顶点),则$\angle1+\angle2$的度数和为(

A.$108^{\circ}$
B.$180^{\circ}$
C.$252^{\circ}$
D.$288^{\circ}$
D
)
A.$108^{\circ}$
B.$180^{\circ}$
C.$252^{\circ}$
D.$288^{\circ}$
答案:
[变式训练] D [解析]
∵五边形$ABCDE$是正五边形,$\angle A = \angle B = \angle C = \angle D = \angle E = \frac{(5 - 2)×180^{\circ}}{5} = 108^{\circ}$,$\therefore\angle A+\angle B+\angle C+\angle D = 108^{\circ}×4 = 432^{\circ}$。
∵六边形的内角和为$(6 - 2)×180^{\circ} = 720^{\circ}$,$\therefore\angle1+\angle2 = 720^{\circ} - 432^{\circ} = 288^{\circ}$。
∵五边形$ABCDE$是正五边形,$\angle A = \angle B = \angle C = \angle D = \angle E = \frac{(5 - 2)×180^{\circ}}{5} = 108^{\circ}$,$\therefore\angle A+\angle B+\angle C+\angle D = 108^{\circ}×4 = 432^{\circ}$。
∵六边形的内角和为$(6 - 2)×180^{\circ} = 720^{\circ}$,$\therefore\angle1+\angle2 = 720^{\circ} - 432^{\circ} = 288^{\circ}$。
2.(2025·安徽)在如图所示的$□ ABCD$中,$E$,$G$分别为边$AD$,$BC$的中点,点$F$,$H$分别在边$AB$,$CD$上移动(不与端点重合),且满足$AF = CH$,则下列为定值的是(

A.四边形$EFGH$的周长
B.$\angle EFG$的大小
C.四边形$EFGH$的面积
D.线段$FH$的长
C
)
A.四边形$EFGH$的周长
B.$\angle EFG$的大小
C.四边形$EFGH$的面积
D.线段$FH$的长
答案:
2.C [解析]连接$EG$,在$□ ABCD$ 中,$E,G$分别为$AD,BC$中点。 $\because AD//BC$且$AD = BC$,$AE=\frac{1}{2}AD$,$BG=\frac{1}{2}BC$,$\therefore AE//BG$且$AE = BG$,$\therefore$四边形$ABGE$是平行四边形,$\therefore AB//EG$。同理$EG//CD$,且$EG = AB = CD$,$\therefore$四边形$DCGE$是平行四边形,则$\triangle GEF$与$\triangle GEH$的面积分别为$□ AB - GE$与$□ EGCD$面积的一半,四边形$EFGH$的面积是$S_{\triangle GEF}+S_{\triangle GEH}$,$\therefore$四边形$EFGH$的面积始终为$□ ABCD$面积的一半,是定值,故C正确。$EF,FG$等边长随$F,H$移动变化,周长不定,故A错误;$\angle EFG$大小随$F$移动改变,故B错误;$FH$长度随$F,H$移动改变,故D错误。
中,$E,G$分别为$AD,BC$中点。 $\because AD//BC$且$AD = BC$,$AE=\frac{1}{2}AD$,$BG=\frac{1}{2}BC$,$\therefore AE//BG$且$AE = BG$,$\therefore$四边形$ABGE$是平行四边形,$\therefore AB//EG$。同理$EG//CD$,且$EG = AB = CD$,$\therefore$四边形$DCGE$是平行四边形,则$\triangle GEF$与$\triangle GEH$的面积分别为$□ AB - GE$与$□ EGCD$面积的一半,四边形$EFGH$的面积是$S_{\triangle GEF}+S_{\triangle GEH}$,$\therefore$四边形$EFGH$的面积始终为$□ ABCD$面积的一半,是定值,故C正确。$EF,FG$等边长随$F,H$移动变化,周长不定,故A错误;$\angle EFG$大小随$F$移动改变,故B错误;$FH$长度随$F,H$移动改变,故D错误。
2.C [解析]连接$EG$,在$□ ABCD$
 中,$E,G$分别为$AD,BC$中点。 $\because AD//BC$且$AD = BC$,$AE=\frac{1}{2}AD$,$BG=\frac{1}{2}BC$,$\therefore AE//BG$且$AE = BG$,$\therefore$四边形$ABGE$是平行四边形,$\therefore AB//EG$。同理$EG//CD$,且$EG = AB = CD$,$\therefore$四边形$DCGE$是平行四边形,则$\triangle GEF$与$\triangle GEH$的面积分别为$□ AB - GE$与$□ EGCD$面积的一半,四边形$EFGH$的面积是$S_{\triangle GEF}+S_{\triangle GEH}$,$\therefore$四边形$EFGH$的面积始终为$□ ABCD$面积的一半,是定值,故C正确。$EF,FG$等边长随$F,H$移动变化,周长不定,故A错误;$\angle EFG$大小随$F$移动改变,故B错误;$FH$长度随$F,H$移动改变,故D错误。
中,$E,G$分别为$AD,BC$中点。 $\because AD//BC$且$AD = BC$,$AE=\frac{1}{2}AD$,$BG=\frac{1}{2}BC$,$\therefore AE//BG$且$AE = BG$,$\therefore$四边形$ABGE$是平行四边形,$\therefore AB//EG$。同理$EG//CD$,且$EG = AB = CD$,$\therefore$四边形$DCGE$是平行四边形,则$\triangle GEF$与$\triangle GEH$的面积分别为$□ AB - GE$与$□ EGCD$面积的一半,四边形$EFGH$的面积是$S_{\triangle GEF}+S_{\triangle GEH}$,$\therefore$四边形$EFGH$的面积始终为$□ ABCD$面积的一半,是定值,故C正确。$EF,FG$等边长随$F,H$移动变化,周长不定,故A错误;$\angle EFG$大小随$F$移动改变,故B错误;$FH$长度随$F,H$移动改变,故D错误。 3.(2020·安徽)在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片$ABCD$沿过点$A$的直线折叠,使得点$B$落在$CD$上的点$Q$处,折痕为$AP$;再将$\triangle PCQ$,$\triangle ADQ$分别沿$PQ$,$AQ$折叠,此时点$C$,$D$落在$AP$上的同一点$R$处。请完成下列探究:

(1)$\angle PAQ$的大小为
(2)当四边形$APCD$是平行四边形时,$\frac{AB}{QR}$的值为

(1)$\angle PAQ$的大小为
30
$^{\circ}$;(2)当四边形$APCD$是平行四边形时,$\frac{AB}{QR}$的值为
√3
。
答案:
3.
(1)$30$
(2)$\sqrt{3}$ [解析]
(1)由折叠的性质可得,$\angle B = \angle AQP$,$\angle DAQ = \angle QAP = \angle PAB$,$\angle DQA = \angle AQR$,$\angle CQP = \angle PQR$,$\angle D = \angle ARQ$,$\angle C = \angle QRP$。$\because\angle QRA + \angle QRP = 180^{\circ}$,$\therefore\angle D + \angle C = 180^{\circ}$,$\therefore AD//BC$,$\therefore\angle B + \angle DAB = 180^{\circ}$。$\because\angle DQR + \angle CQR = 180^{\circ}$,$\therefore\angle DQA + \angle CQP = 90^{\circ}$,$\therefore\angle AQP = 90^{\circ}$,$\angle B = \angle AQP = 90^{\circ}$,$\angle DAB = 90^{\circ}$,$\therefore\angle DAQ = \angle QAP = \angle PAB = 30^{\circ}$。
(2)由折叠的性质可得,$AD = AR$,$CP = PR$。$\because$四边形$APCD$是平行四边形,$\therefore AD = PC$,$\therefore AR = PR$。又$\because\angle AQP = 90^{\circ}$,$\therefore QR = \frac{1}{2}AP$。$\because\angle PAB = 30^{\circ}$,$\angle B = 90^{\circ}$,$\therefore AP = 2PB$,$AB = \sqrt{3}PB$,$\therefore PB = QR$,$\therefore\frac{AB}{QR}=\sqrt{3}$。
(1)$30$
(2)$\sqrt{3}$ [解析]
(1)由折叠的性质可得,$\angle B = \angle AQP$,$\angle DAQ = \angle QAP = \angle PAB$,$\angle DQA = \angle AQR$,$\angle CQP = \angle PQR$,$\angle D = \angle ARQ$,$\angle C = \angle QRP$。$\because\angle QRA + \angle QRP = 180^{\circ}$,$\therefore\angle D + \angle C = 180^{\circ}$,$\therefore AD//BC$,$\therefore\angle B + \angle DAB = 180^{\circ}$。$\because\angle DQR + \angle CQR = 180^{\circ}$,$\therefore\angle DQA + \angle CQP = 90^{\circ}$,$\therefore\angle AQP = 90^{\circ}$,$\angle B = \angle AQP = 90^{\circ}$,$\angle DAB = 90^{\circ}$,$\therefore\angle DAQ = \angle QAP = \angle PAB = 30^{\circ}$。
(2)由折叠的性质可得,$AD = AR$,$CP = PR$。$\because$四边形$APCD$是平行四边形,$\therefore AD = PC$,$\therefore AR = PR$。又$\because\angle AQP = 90^{\circ}$,$\therefore QR = \frac{1}{2}AP$。$\because\angle PAB = 30^{\circ}$,$\angle B = 90^{\circ}$,$\therefore AP = 2PB$,$AB = \sqrt{3}PB$,$\therefore PB = QR$,$\therefore\frac{AB}{QR}=\sqrt{3}$。
查看更多完整答案,请扫码查看


