《2026年决胜中考数学安徽专版》

典例 1（2025·安徽模拟）
计算：$4\sin 30^{\circ}-\sqrt{8}+(\pi - 2025)^{0}+(-1)^{2025}$。

答案： 解:原式=4×$\frac{1}{2}$−2$\sqrt{2}$+1+(−1)=2−2$\sqrt{2}$+1−1=2−2$\sqrt{2}$。
[解析]先运用含特殊角三角函数的混合运算、二次根式的性质、零次幂、负数的奇次幂化简，然后再计算即可。

典例 2（2025·太湖县二模）
先化简，再求值：$(2x + 1)(1 - 2x) - 2(x + 2)(x - 4)+(2x - 1)^{2}$，其中$x = -\sqrt{3}$。

答案： 解:原式=1−4x²−2(x²−4x+2x−8)+4x²−4x+1=1−4x²−2x²+8x−4x+16+4x²−4x+1=−2x²+18，当x=−$\sqrt{3}$时，原式=−2×(−$\sqrt{3}$)²+18=−2×3+18=−6+18=12。
[解析]先根据平方差公式，多项式乘多项式，完全平方公式进行计算，再合并同类项，最后代入求出答案即可。

典例 3（2025·潜山市三模）
先化简，再求值：$(\frac{2x^{2}-2x + 1}{x}-1)÷\frac{x^{2}-2x + 1}{x}$，其中$x = \sqrt{2}+1$。

答案： 解:原式=$\frac{2x^{2}-2x+1-x · (x-1)^{2}}{x} ÷ \frac{(x-1)^{2}}{x}=\frac{2x^{2}-3x+1}{x} · \frac{x}{(x-1)^{2}}=\frac{(2x-1)(x-1)}{x} · \frac{x}{(x-1)^{2}}=\frac{2x-1}{x-1}$，当x=$\sqrt{2}$+1时，原式=$\frac{2(\sqrt{2}+1)−1}{\sqrt{2}+1−1}$=$\frac{2\sqrt{2}+1}{\sqrt{2}}$=2+$\frac{\sqrt{2}}{2}$。
[解析]利用分式的相应法则对式子进行化简，再代入相应的值运算即可。

典例 4（2025·安庆模拟）
用适当的方法解方程：$2x^{2}-4x + 1 = 0$。

答案： 解:
∵一元二次方程为2x²−4x+1=0，
∴a=2，b=−4，c=1，
∴Δ=b²−4ac=(−4)²−4×2×1=8＞0，
∴x=$\frac{−b±\sqrt{b²−4ac}}{2a}$=$\frac{−(−4)±\sqrt{8}}{2×2}$=$\frac{2±\sqrt{2}}{2}$，
∴x₁=1+$\frac{\sqrt{2}}{2}$，x₂=1−$\frac{\sqrt{2}}{2}$。
[解析]利用公式法进行解方程即可。

典例 5
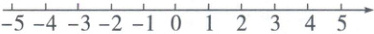
解不等式组$\begin{cases}2(x + 1) ＞ x·s①,\\1 - 2x\geqslant\frac{x + 7}{2}·s②,\end{cases}$并把它的解集在数轴上表示出来。

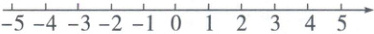
答案：
解:解不等式①得，x＞−2，解不等式②得，x≤−1，
∴不等式组的解集为−2＜x≤−1。在数轴上表示如图所示。

[解析]分别求出不等式组中两个不等式的解集，找出公共部分，表示在数轴上即可。