《2026年步步高精准讲练高中数学选择性必修第二册人教版》

我国魏晋时期的科学家刘徽创立了“割圆术”，实施“以直代曲”的近似计算，用正 $ n $ 边形进行“内外夹逼”的办法求出了圆周率 $ \pi $ 的精度较高的近似值，这是我国最优秀的传统科学文化之一. 借用“以直代曲”的近似计算方法，在切点附近，可以用函数图象的切线近似代替在切点附近的曲线来近似计算. 设 $ f(x) = e^{x^2} $，则 $ f'(x) = $$2xe^{x^2}$，其在点 $ (0,1) $ 处的切线方程为$y = 1$.

答案： $2xe^{x^2}$ $y = 1$

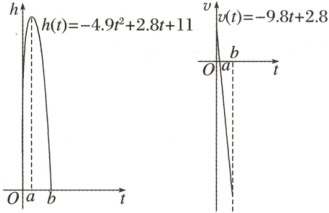
观察下面一次跳水的运动轨迹以及其导数的图象，试说明运动员从起跳到最高点，以及从最高点到入水这两段时间的运动状态有什么区别？如何从数学上刻画这种区别？

答案： 通过观察图象，可以发现
(1)从起跳到最高点，运动员离水面的高度h随时间t的增加而增加，即h(t)单调递增，相应地，v(t)=h'(t)＞0；
(2)从最高点到入水，运动员离水面的高度h随时间t的增加而减小，即h(t)单调递减，相应地，v(t)=h'(t)＜0。

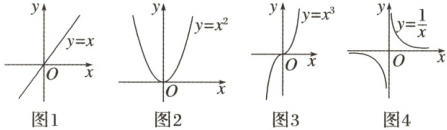
观察下面几个图象，探究函数的单调性和导数的正负的关系。

答案：
(1)函数y=x的定义域为R，并且在定义域上是增函数，其导数y'=1 ＞0；
(2)函数y=x²的定义域为R，在(-∞,0)上单调递减，在(0,+∞)上单调递增。而y'=2x，当x＜0时，其导数y'＜0；当x＞0时，其导数y'＞0；当x =0时，其导数y'=0；
(3)函数y=x³的定义域为R，在定义域上为增函数。而y'=3x²，当x≠0 时，其导数y'＞0；当x=0时，其导数y'=0；
(4)函数y=$\frac{1}{x}$的定义域为(-∞,0)∪(0,+∞)，在(-∞,0)上单调递减，在(0,+∞)上单调递减，而y'=-$\frac{1}{x²}$，因为x≠0，所以y'＜0。
从以上四个函数的单调性及其导数符号的关系上说明，在某个区间(a，b)上，如果f'(x)＞0，那么函数y=f(x)在这个区间上单调递增；如果f'(x)＜0，那么函数y=f(x)在这个区间上单调递减。

函数的单调性与其导数的正负之间的关系
定义在区间$(a,b)$上的函数$y = f(x)$：

答案： 增　减

利用导数判断下列函数的单调性：
(1)$f(x)=\frac{1}{3}x^{3}-x^{2}+2x - 5$；
(2)$f(x)=x-\frac{1}{x}-\ln x$；
(3)$f(x)=x - e^{x}(x ＞ 0)$。
反思感悟：

答案： 解　
(1)因为f(x)=$\frac{1}{3}$x³−x²+2x−5，所以f′(x)=x²−2x+2=(x−1)²+1＞0，所以函数f(x)=$\frac{1}{3}$x³ −x²+2x−5在R上单调递增。
(2)因为f(x)=x−$\frac{1}{x}$−lnx，x∈(0,+∞)，所以f'(x)=1+$\frac{1}{x²}$-$\frac{1}{x}$=$\frac{x²−x+1}{x²}$=$\frac{(x−\frac{1}{2})²+\frac{3}{4}}{x²}$＞0，所以f(x)=x−$\frac{1}{x}$−lnx在(0,+∞)上单调递增。
(3)因为f(x)=x−e^x，x∈(0,+∞)，所以f'(x)=1−e^x＜0，所以f(x)=x−e^x在(0,+∞)上单调递减。