《2026年步步高精准讲练高中数学选择性必修第二册人教版》

(1)已知等比数列$\{ a_{n}\}$的公比$q=\frac{1}{3}$，且$a_{1}+a_{3}+a_{5}+·s +a_{99}=90$，则$a_{1}+a_{2}+a_{3}+·s +a_{100}=$120。
(2)记等比数列$\{ a_{n}\}$的前n项和为$S_{n}$，若$S_{4}=3,S_{8}=9$，则$S_{12}$等于(C)
A. 12
B. 18
C. 21
D. 27

答案：
(1)120
(2)C

《算法统宗》是中国古代数学名著，程大位著，共17卷，书中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还。”大致意思是：有一个人要到距离出发地378里的地方，第一天健步行走，从第二天起因脚痛每天走的路程为前一天的一半，走了6天后到达目的地。那么该人第一天所走路程里数为(C)

A.96
B.126
C.192
D.252

答案： C [由题意得，该人每天走的路程形成以$a_1$为首项，以$\frac{1}{2}$为公比的等比数列，
因为该人6天后到达目的地，则有
$S_6=\frac{a_1\left[1-\left(\frac{1}{2}\right)^6\right]}{1-\frac{1}{2}}=378$，
解得$a_1=192$，所以该人第一天所走路程里数为192.]

中国三大名楼之一的黄鹤楼因其独特的建筑结构而闻名，其外观有五层而实际上内部有九层，隐喻“九五至尊”之意，现打算在黄鹤楼内部挂灯笼进行装饰，若在黄鹤楼内部九层塔楼共挂1533盏灯笼，且相邻的两层中，下一层的灯笼数是上一层灯笼数的两倍，则内部塔楼的顶层应挂3盏灯笼。

答案： 3 解 记第$n$个正方形的边长为$b_n$，由题意可知当$n \geq 2$时，
$b_n^2=2 × \left(\frac{b_{n-1}}{2}\right)^2=\frac{1}{2}b_{n-1}^2$，
则$a_n=\frac{1}{2}a_{n-1}$，
所以数列$\{a_n\}$是以$a_1=4$为首项，$q=\frac{1}{2}$为公比的等比数列，
即$a_n=4 × \left(\frac{1}{2}\right)^{n-1}=2^{3-n}$.
$S_{2024}=\frac{4 × \left[1-\left(\frac{1}{2}\right)^{2024}\right]}{1-\frac{1}{2}}$
$=8 × \left(1-\frac{1}{2^{2024}}\right)=8-\frac{1}{2^{2021}}$.

在等腰直角三角形ABC中，$B=\frac{\pi}{2},AB = a$，以AB为斜边作等腰直角三角形$AB_{1}B$，再以$AB_{1}$为斜边作等腰直角三角形$AB_{2}B_{1}$，依此类推，记$\triangle ABC$的面积为$S_{1}$，依次所得三角形的面积分别为$S_{2},S_{3},·s$，若$S_{1}+S_{2}+·s +S_{8}=\frac{255}{32}$，则a等于(B)

A.2
B.$2\sqrt{2}$
C.3
D.4
反思感悟：

答案： B [由题知$AB_1=\frac{\sqrt{2}}{2}AB$，
$AB_2=\frac{\sqrt{2}}{2}AB_1$，$·s$，$AB_{n+1}=\frac{\sqrt{2}}{2}AB_n$，
$S_1=\frac{1}{2}AB^2=\frac{1}{2}a^2$，
$S_n=\frac{1}{2}AB_{n-1}^2(n \geq 2)$，
所以$\frac{S_{n+1}}{S_n}=\left(\frac{AB_n}{AB_{n-1}}\right)^2=\frac{1}{2}(n \geq 2)$，
又$S_2=\frac{1}{4}a^2=\frac{1}{2}S_1$，
所以数列$\{S_n\}$是首项为$\frac{1}{2}a^2$，公比为$\frac{1}{2}$的等比数列，
所以$S_1+S_2+S_3+·s+S_8=\frac{\frac{1}{2}a^2\left[1-\left(\frac{1}{2}\right)^8\right]}{1-\frac{1}{2}}=\frac{255}{32}$，
所以$a=2\sqrt{2}$(负值舍去).]

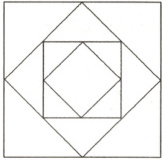
如图，画一个边长为2的正方形，再将此正方形各边的中点相连得到第2个正方形，以此类推，记第n个正方形的面积为$a_{n}$，数列$\{ a_{n}\}$的前n项和为$S_{n}$。求$\{ a_{n}\}$的通项公式及$S_{2024}$。

答案： 解 记第$n$个正方形的边长为$b_n$，由题意可知当$n \geq 2$时，$b_n^2=2 × \left(\frac{b_{n-1}}{2}\right)^2=\frac{1}{2}b_{n-1}^2$，则$a_n=\frac{1}{2}a_{n-1}$，所以数列$\{a_n\}$是以$a_1=4$为首项，$q=\frac{1}{2}$为公比的等比数列，即$a_n=4 × \left(\frac{1}{2}\right)^{n-1}=2^{3-n}$.
$S_{2024}=\frac{4 × \left[1-\left(\frac{1}{2}\right)^{2024}\right]}{1-\frac{1}{2}}=8 × \left(1-\frac{1}{2^{2024}}\right)=8-\frac{1}{2^{2021}}$.