2026年步步高精准讲练高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年步步高精准讲练高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
求曲线 $ y = \frac{1}{x} $ 在点 $ (2, \frac{1}{2}) $ 处的切线方程.
答案:
曲线在点$(2,\frac{1}{2})$处的切线的斜率$k = \lim_{\Delta x \to 0} \frac{\frac{1}{2 + \Delta x} - \frac{1}{2}}{\Delta x} = \lim_{\Delta x \to 0} \frac{-1}{2(2 + \Delta x)} = -\frac{1}{4}$,由直线的点斜式方程可得切线方程为$y - \frac{1}{2} = -\frac{1}{4}(x - 2)$,即$x + 4y - 4 = 0$.
函数的单调性和导数有什么关系?
导数值的大小与函数变化的快慢有什么关系?
导数值的大小与函数变化的快慢有什么关系?
答案:
如图,

当$t = t_0$时,函数的图象在$t = t_0$处的切线$l_0$平行于$t$轴,即$h^{\prime}(t_0) = 0$,这时,在$t = t_0$附近曲线比较平坦,几乎没有升降.
当$t = t_1$时,函数的图象在$t = t_1$处的切线$l_1$的斜率$h^{\prime}(t_1) < 0$,这时,在$t = t_1$附近曲线下降,即函数在$t = t_1$附近单调递减.
当$t = t_2$时,函数的图象在$t = t_2$处的切线$l_2$的斜率$h^{\prime}(t_2) < 0$,这时,在$t = t_2$附近曲线下降,即函数在$t = t_2$附近单调递减.
通过研究在$t = t_1$和$t = t_2$处的切线$l_1$和$l_2$,发现切线$l_1$的倾斜程度小于切线$l_2$的倾斜程度,这说明函数在$t = t_1$附近比在$t = t_2$附近下降得缓慢.
如图,

当$t = t_0$时,函数的图象在$t = t_0$处的切线$l_0$平行于$t$轴,即$h^{\prime}(t_0) = 0$,这时,在$t = t_0$附近曲线比较平坦,几乎没有升降.
当$t = t_1$时,函数的图象在$t = t_1$处的切线$l_1$的斜率$h^{\prime}(t_1) < 0$,这时,在$t = t_1$附近曲线下降,即函数在$t = t_1$附近单调递减.
当$t = t_2$时,函数的图象在$t = t_2$处的切线$l_2$的斜率$h^{\prime}(t_2) < 0$,这时,在$t = t_2$附近曲线下降,即函数在$t = t_2$附近单调递减.
通过研究在$t = t_1$和$t = t_2$处的切线$l_1$和$l_2$,发现切线$l_1$的倾斜程度小于切线$l_2$的倾斜程度,这说明函数在$t = t_1$附近比在$t = t_2$附近下降得缓慢.
若 $ f'(x_0) = 0 $,则函数在 $ x = x_0 $ 处切线斜率 $ k = $
若 $ f'(x_0) > 0 $,则函数在 $ x = x_0 $ 处切线斜率 $ k $
若 $ f'(x_0) < 0 $,则函数在 $ x = x_0 $ 处切线斜率 $ k $
0
;若 $ f'(x_0) > 0 $,则函数在 $ x = x_0 $ 处切线斜率 $ k $
>
0,且函数在 $ x = x_0 $ 附近单调递增
,且 $ f'(x_0) $ 越大,说明函数图象变化得越快;若 $ f'(x_0) < 0 $,则函数在 $ x = x_0 $ 处切线斜率 $ k $
<
0,且函数在 $ x = x_0 $ 附近单调递减
,且 $ |f'(x_0)| $ 越大,说明函数图象变化得越快.
答案:
$0$ $>$ 增 $<$ 减
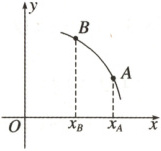
已知 $ y = f(x) $ 的图象如图所示,则 $ f'(x_A) $ 与 $ f'(x_B) $ 的大小关系是(
A.$ f'(x_A) > f'(x_B) $
B.$ f'(x_A) < f'(x_B) $
C.$ f'(x_A) = f'(x_B) $
D.不能确定
反思感悟:
B
)
A.$ f'(x_A) > f'(x_B) $
B.$ f'(x_A) < f'(x_B) $
C.$ f'(x_A) = f'(x_B) $
D.不能确定
反思感悟:
答案:
B [由导数的几何意义,$f^{\prime}(x_A)$,$f^{\prime}(x_B)$分别是函数在点$A$,$B$处切线的斜率,由图象可知$f^{\prime}(x_A) < f^{\prime}(x_B)$.]
已知函数 $ f(x) $ 在 $ \mathbf{R} $ 上可导,其部分图象如图所示,设 $ \frac{f(2) - f(1)}{2 - 1} = a $,则下列不等式正确的是(
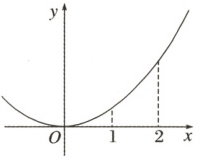
A.$ f'(1) < f'(2) < a $
B.$ f'(1) < a < f'(2) $
C.$ f'(2) < f'(1) < a $
D.$ a < f'(1) < f'(2) $
B
)
A.$ f'(1) < f'(2) < a $
B.$ f'(1) < a < f'(2) $
C.$ f'(2) < f'(1) < a $
D.$ a < f'(1) < f'(2) $
答案:
B
如何利用 $ f'(x_0) $ 的定义以及函数的概念给出导函数的概念?
答案:
如果函数$y = f(x)$在开区间$(a,b)$内的每点处都有导数,即任给$x_0 \in (a,b)$,总有$\lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = f^{\prime}(x_0)$,从而对开区间$(a,b)$内的每一个值$x_0$,都有唯一确定的函数值$f^{\prime}(x_0)$与$x_0$对应,所以在开区间$(a,b)$内,$f^{\prime}(x)$构成一个新的函数——导函数$f^{\prime}(x)$.
从求函数 $ f(x) $ 在 $ x = x_0 $ 处导数的过程可以看到,当 $ x = x_0 $ 时,$ f'(x_0) $ 是一个唯一确定的数. 这样,当 $ x $ 变化时,$ y = f'(x) $ 就是 $ x $ 的函数,我们称它为 $ y = f(x) $ 的
导函数
(简称导数). $ y = f(x) $ 的导函数记作$f^{\prime}(x)$
或$y^{\prime}$
,即 $ f'(x) = y' = $$\lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$
.
答案:
导函数$f^{\prime}(x)$ $y^{\prime}$
$\lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$
$\lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$
查看更多完整答案,请扫码查看


