《2026年步步高精准讲练高中数学选择性必修第二册人教版》

问题3 在点$P_0(1,1)$的附近任取一点$P(x,x^2)$,考察抛物线$f(x)=x^2$的割线$P_0P$有什么变化趋势?

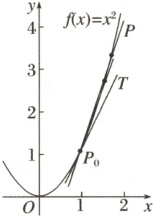
答案： 当点$P$无限趋近于点$P_0$时，割线$P_0P$无限趋近于一个确定的位置.

例3 求抛物线$f(x)=x^2-2x+3$在点$(1,2)$处的切线方程.
延伸探究 本例函数不变,求与$2x-y+4=0$平行的该曲线的切线方程.
反思感悟:.

答案： 解　由$\frac{f(1+\Delta x)-f(1)}{\Delta x}=\frac{(1+\Delta x)^2-2(1+\Delta x)+3 - 2}{\Delta x}=\Delta x$，
可得切线的斜率为$k=\lim_{\Delta x\rightarrow0}\Delta x=0$.
所以切线的方程为$y - 2=0×(x - 1)$，
即$y = 2$.
延伸探究　解　设切点坐标为$(x_0,x_0^2-2x_0+3)$，
故$\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\frac{(x_0+\Delta x)^2-2(x_0+\Delta x)+3 - x_0^2+2x_0 - 3}{\Delta x}=2x_0-2+\Delta x$，
所以切线的斜率
$k=\lim_{\Delta x\rightarrow0}(2x_0-2+\Delta x)=2x_0-2$，
故有$2x_0-2=2$，解得$x_0=2$，所以切点坐标为$(2,3)$，所求切线方程为$2x - y - 1=0$.

跟踪训练3 求抛物线$f(x)=x^2-x$在点$(2,2)$处的切线方程.

答案： 解　$f(2+\Delta x)-f(2)=(2+\Delta x)^2-(2+\Delta x)-2=3\Delta x+(\Delta x)^2$，
所以切线的斜率
$k=\lim_{\Delta x\rightarrow0}\frac{f(2+\Delta x)-f(2)}{\Delta x}=\lim_{\Delta x\rightarrow0}\frac{3\Delta x+(\Delta x)^2}{\Delta x}=\lim_{\Delta x\rightarrow0}(3+\Delta x)=3$.
则切线方程为$y - 2=3(x - 2)$，
即$3x - y - 4=0$.