《2026年南方凤凰台5A新考案高中数学二轮基础版》

例 2 （2025·赣州期末）已知$\triangle ABC$的内角$A,B,C$所对的边分别为$a,b,c$，且$\sin\frac{A}{2}·(\cos\frac{A}{2}-\sqrt{3}\sin\frac{A}{2})+\cos\frac{A}{2}(\sqrt{3}\cos\frac{A}{2}+\sin\frac{A}{2})=2$.
（1）求$A$；
（2）若$a = 2$，$\cos A+\cos(B - C)=\sqrt{2}\sin 2B·\sin C$，求$\triangle ABC$的周长.

答案： 例2【解答】
(1)由$\sin\frac{A}{2}(\cos\frac{A}{2}-\sqrt{3}\sin\frac{A}{2})+\cos\frac{A}{2}·(\sqrt{3}\cos\frac{A}{2}+\sin\frac{A}{2})=2$，得$2\sin\frac{A}{2}\cos\frac{A}{2}+\sqrt{3}(\cos^{2}\frac{A}{2}-\sin^{2}\frac{A}{2})=2$，从而$\sin A+\sqrt{3}\cos A=2$，化简得$\sin(A+\frac{\pi}{3})=1$.因为$0＜A＜\pi$，所以$\frac{\pi}{3}＜A+\frac{\pi}{3}＜\frac{4\pi}{3}$，故$A=\frac{\pi}{6}$.
(2)由$\cos A+\cos(B - C)=\sqrt{2}\sin B\sin C$，可得$\cos(B - C)-\cos(B + C)=2\sqrt{2}\sin B\cos B\sin C$，即$(\cos B\cos C+\sin B·\sin C)-(\cos B\cos C-\sin B\sin C)=2\sqrt{2}\sin B\cos B\sin C$，即$2\sin B\sin C=2\sqrt{2}\sin B\cos B\sin C$.又因为$\sin B\sin C\neq0$，所以$\cos B=\frac{\sqrt{2}}{2}$.又因为$B\in(0,\pi)$，所以$B=\frac{\pi}{4}$，所以$C=\frac{7\pi}{12}$，且$\sin\frac{7\pi}{12}=\sin(\frac{\pi}{3}+\frac{\pi}{4})=\frac{\sqrt{2}}{2}×(\frac{\sqrt{3}}{2}+\frac{1}{2})=\frac{\sqrt{6}+\sqrt{2}}{4}$.在$\triangle ABC$中，由正弦定理可得$\frac{2}{\sin\frac{\pi}{6}}=\frac{b}{\sin\frac{\pi}{4}}=\frac{c}{\sin\frac{7\pi}{12}}=4$，解得$b=2\sqrt{2}$，$c=\sqrt{2}+\sqrt{6}$，故$\triangle ABC$的周长为$2+3\sqrt{2}+\sqrt{6}$.

变式 2 设$a,b,c$分别为$\triangle ABC$的内角$A,B,C$的对边，已知$c^{2}=3(a^{2}-b^{2})$，且$\tan C = 3$，则$B =$$\frac{\pi}{4}$.

答案： 变式2$\frac{\pi}{4}$【解析】方法一：(正弦平方差公式)由正弦定理得$\sin^{2}C=3(\sin^{2}A-\sin^{2}B)=3\sin(A - B)\sin(A + B)\Rightarrow\sin C=3\sin(A - B)=3\sin(\pi-2B - C)=3\sin(2B + C)$.又$\tan C=3$，所以$\sin C=3\cos C=3\sin(2B + C)$，可得$\cos C=\sin(2B + C)$，所以$2B=\frac{\pi}{2}$，即$B=\frac{\pi}{4}$.
方法二：(边转化为角)$c^{2}=3(a^{2}-b^{2})\Rightarrow\sin^{2}C=3(\sin^{2}A-\sin^{2}B)=\tan C(\sin^{2}A-\sin^{2}B)=\frac{\sin C}{\cos C}·(\sin^{2}A-\sin^{2}B)=\sin C\cos C=\sin^{2}(B + C)-\sin^{2}B=(\sin B\cos C+\cos B\sin C)^{2}-\sin^{2}B=\sin^{2}B\cos^{2}C+\cos^{2}B\sin^{2}C+2\sin B\cos C\cos B\sin C-\sin^{2}B=-\sin^{2}B\sin^{2}C+\cos^{2}B\sin^{2}C+2\sin B\cos C\cos B\sin C\Rightarrow\cos C=(\cos^{2}B-\sin^{2}B)·\sin C+2\sin B\cos C\cos B=(\cos^{2}B-\sin^{2}B)\sin C\Rightarrow(\cos B-\sin B)^{2}=3(\cos B+\sin B)(\cos B-\sin B)$.当$\cos B-\sin B=0$时，$B=\frac{\pi}{4}$；当$\cos B-\sin B\neq0$时，$\cos B-\sin B=3(\cos B+\sin B)$，可得$\tan B=-\frac{1}{2}\Rightarrow B＞90^{\circ}$，即$b＞a\Rightarrow c^{2}=3(a^{2}-b^{2})＜0$矛盾.所以$B=\frac{\pi}{4}$.

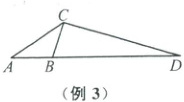
例 3 （2025·南昌信息卷）在$\triangle ABC$中，内角$A,B,C$所对的边分别为$a,b,c$，已知$a=\sqrt{3}$，$3\cos 2A-\cos 2B = 2$.
（1）求$b$；
（2）如图，延长$AB$，若$BD = 3c$，$CD\perp BC$，求$c$.

答案： 例3【解答】
(1)因为$3\cos2A-\cos2B=2$，所以$3(1-2\sin^{2}A)-(1-2\sin^{2}B)=2$，可得$\sin^{2}B=3\sin^{2}A$.由正弦定理得$b^{2}=3a^{2}$.又因为$a=\sqrt{3}$，所以$b=3$.
(2)因为$\angle ABC+\angle CBD=\pi$，所以$\cos\angle ABC+\cos\angle CBD=0$.在$\triangle BCD$中，$BD=3c$，$a=BC=\sqrt{3}$，且$CD\perp BC$，所以$\cos\angle CBD=\frac{\sqrt{3}}{3c}$.在$\triangle ABC$中，由余弦定理可得$\cos\angle ABC=\frac{c^{2}+3-9}{2c×\sqrt{3}}$，所以$\frac{c^{2}-6}{2c×\sqrt{3}}+\frac{\sqrt{3}}{3c}=0$，即$\frac{c^{2}-6}{2c}+\frac{1}{c}=0$，解得$c=2$.