2026年南方凤凰台5A新考案高中数学二轮基础版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年南方凤凰台5A新考案高中数学二轮基础版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
例1 (2025·辽宁省三模)甲、乙两人进行一场网球比赛,比赛采用三局两胜制,每局都没有平局,且甲第一局获胜的概率为p(0 < p < 1)。从第二局开始,若上一局甲获胜,则下一局甲获胜的概率为p²,若上一局甲未获胜,则下一局甲获胜的概率为1 - p。
(1)当p = $\frac{1}{2}$时,求甲第二局获胜的概率。
(2)设甲第一局未获胜且第二局获胜的概率为$\frac{1}{9}$。
①求p;
②记这场比赛需要进行的局数为X,求X的分布列与期望。
(1)当p = $\frac{1}{2}$时,求甲第二局获胜的概率。
(2)设甲第一局未获胜且第二局获胜的概率为$\frac{1}{9}$。
①求p;
②记这场比赛需要进行的局数为X,求X的分布列与期望。
答案:
(1)设$A_i$=“甲第$i$局获胜”,其中$i=1,2,3$,依题意得$P(A_1)=p$,当$p=\frac{1}{2}$时,由全概率公式得$P(A_2)=P(A_1A_2)+P(\overline{A_1}A_2)=P(A_1)P(A_2|A_1)+P(\overline{A_1})P(A_2|\overline{A_1})=p· p^2+(1-p)=\left(\frac{1}{2}\right)^3+\left(1-\frac{1}{2}\right)^2=\frac{3}{8}$,所以甲第二局获胜的概率为$\frac{3}{8}$。
(2)①甲第一局未获胜且第二局获胜的概率为$(1-p)^2$,依题意
得$(1-p)^2=\frac{1}{9}$,解得$p=\frac{2}{3}$。
②$X$的可能取值为$2,3$,则$P(X=2)=P(A_1A_2)+P(\overline{A_1}\overline{A_2})=p· p^2+(1-p)p=\left(\frac{2}{3}\right)^3+\frac{1}{3}×\frac{2}{3}=\frac{14}{27}$,$P(X=3)=P(A_1\overline{A_2}A_3)+P(\overline{A_1}A_2\overline{A_3})+P(\overline{A_1}\overline{A_2}A_3)=p(1-p^2)(1-p)+(1-p)(1-p)p^2+p(1-p)(1-p^2)=1-p^3+p^2-p=1-\left(\frac{2}{3}\right)^3+\left(\frac{2}{3}\right)^2-\frac{2}{3}=\frac{13}{27}$(或$P(X=3)=1-P(X=2)=1-\frac{14}{27}=\frac{13}{27}$),所以$X$的分布
列为
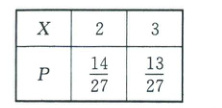
故$E(X)=2×\frac{14}{27}+3×\frac{13}{27}=\frac{67}{27}$。
(1)设$A_i$=“甲第$i$局获胜”,其中$i=1,2,3$,依题意得$P(A_1)=p$,当$p=\frac{1}{2}$时,由全概率公式得$P(A_2)=P(A_1A_2)+P(\overline{A_1}A_2)=P(A_1)P(A_2|A_1)+P(\overline{A_1})P(A_2|\overline{A_1})=p· p^2+(1-p)=\left(\frac{1}{2}\right)^3+\left(1-\frac{1}{2}\right)^2=\frac{3}{8}$,所以甲第二局获胜的概率为$\frac{3}{8}$。
(2)①甲第一局未获胜且第二局获胜的概率为$(1-p)^2$,依题意
得$(1-p)^2=\frac{1}{9}$,解得$p=\frac{2}{3}$。
②$X$的可能取值为$2,3$,则$P(X=2)=P(A_1A_2)+P(\overline{A_1}\overline{A_2})=p· p^2+(1-p)p=\left(\frac{2}{3}\right)^3+\frac{1}{3}×\frac{2}{3}=\frac{14}{27}$,$P(X=3)=P(A_1\overline{A_2}A_3)+P(\overline{A_1}A_2\overline{A_3})+P(\overline{A_1}\overline{A_2}A_3)=p(1-p^2)(1-p)+(1-p)(1-p)p^2+p(1-p)(1-p^2)=1-p^3+p^2-p=1-\left(\frac{2}{3}\right)^3+\left(\frac{2}{3}\right)^2-\frac{2}{3}=\frac{13}{27}$(或$P(X=3)=1-P(X=2)=1-\frac{14}{27}=\frac{13}{27}$),所以$X$的分布
列为

故$E(X)=2×\frac{14}{27}+3×\frac{13}{27}=\frac{67}{27}$。
例2 (2025·永州模拟节选)某校组织“AI模型”知识竞赛,甲、乙两名选手在决赛阶段相遇,决赛阶段共有3道题目,甲、乙同时依次作答,3道题目作答完毕后比赛结束。规定:对同一道题目,若两人同时答对或答错,每人得0分;若一人答对另一人答错,答对的得10分,答错的得 - 10分,比赛结束累加得分为正数者获胜,两人分别独立答题互不影响,每人每次的答题结果也互不影响,若甲、乙两名选手正确回答每道题目的概率分别为$\frac{3}{5}$,$\frac{1}{2}$。
(1)求比赛结束后甲获胜的概率;
(2)求比赛结束后甲获胜的条件下,乙恰好回答对1道题目的概率。
(1)求比赛结束后甲获胜的概率;
(2)求比赛结束后甲获胜的条件下,乙恰好回答对1道题目的概率。
答案:
(1)当甲、乙同时回答第$i(i=1,2,3)$道题时,甲得
分为$X_i$,则$P(X_i=10)=\frac{3}{5}×\frac{1}{2}=\frac{3}{10}$,$P(X_i=0)=\frac{3}{5}×\frac{1}{2}+\frac{2}{5}×\frac{1}{2}=\frac{1}{2}$,$P(X_i=-10)=\frac{2}{5}×\frac{1}{2}=\frac{1}{5}$。比赛结束甲获胜时
的得分$X$可能的取值为$10,20,30$,则$P(X=30)=\left(\frac{3}{10}\right)^3=\frac{27}{1000}$,$P(X=20)=C_3^1×\frac{1}{2}×\left(\frac{3}{10}\right)^2=\frac{27}{200}$,$P(X=10)=C_3^3×\frac{3}{10}×\left(\frac{1}{2}\right)+C_3^1×\frac{3}{10}×\left(\frac{3}{10}\right)^2=\frac{279}{1000}$,所以比赛结束后甲获胜
的概率$P=P(X=30)+P(X=20)+P(X=10)=\frac{27}{1000}+\frac{27}{200}+\frac{279}{1000}=\frac{441}{1000}$。
(2)设$A$=“比赛结束后甲获胜”,$B$=“比赛结束时乙恰好答对一
道题”,$P(AB)=\left(\frac{3}{10}\right)^3× C_3^1×\frac{1}{2}×\left(1-\frac{1}{2}\right)^2+C_3^3×\left(\frac{3}{5}\right)^2×\left(1-\frac{3}{5}\right)× C_3^1×\frac{1}{2}×\left(1-\frac{1}{2}\right)^2=\frac{243}{1000}$,则$P(B|A)=\frac{P(AB)}{P(A)}=\frac{\frac{243}{1000}}{\frac{441}{1000}}=\frac{27}{49}$,所以比赛结束后甲获胜的条件下,乙恰好
回答对1道题目的概率为$\frac{27}{49}$。
(1)当甲、乙同时回答第$i(i=1,2,3)$道题时,甲得
分为$X_i$,则$P(X_i=10)=\frac{3}{5}×\frac{1}{2}=\frac{3}{10}$,$P(X_i=0)=\frac{3}{5}×\frac{1}{2}+\frac{2}{5}×\frac{1}{2}=\frac{1}{2}$,$P(X_i=-10)=\frac{2}{5}×\frac{1}{2}=\frac{1}{5}$。比赛结束甲获胜时
的得分$X$可能的取值为$10,20,30$,则$P(X=30)=\left(\frac{3}{10}\right)^3=\frac{27}{1000}$,$P(X=20)=C_3^1×\frac{1}{2}×\left(\frac{3}{10}\right)^2=\frac{27}{200}$,$P(X=10)=C_3^3×\frac{3}{10}×\left(\frac{1}{2}\right)+C_3^1×\frac{3}{10}×\left(\frac{3}{10}\right)^2=\frac{279}{1000}$,所以比赛结束后甲获胜
的概率$P=P(X=30)+P(X=20)+P(X=10)=\frac{27}{1000}+\frac{27}{200}+\frac{279}{1000}=\frac{441}{1000}$。
(2)设$A$=“比赛结束后甲获胜”,$B$=“比赛结束时乙恰好答对一
道题”,$P(AB)=\left(\frac{3}{10}\right)^3× C_3^1×\frac{1}{2}×\left(1-\frac{1}{2}\right)^2+C_3^3×\left(\frac{3}{5}\right)^2×\left(1-\frac{3}{5}\right)× C_3^1×\frac{1}{2}×\left(1-\frac{1}{2}\right)^2=\frac{243}{1000}$,则$P(B|A)=\frac{P(AB)}{P(A)}=\frac{\frac{243}{1000}}{\frac{441}{1000}}=\frac{27}{49}$,所以比赛结束后甲获胜的条件下,乙恰好
回答对1道题目的概率为$\frac{27}{49}$。
查看更多完整答案,请扫码查看


