《2026年南方凤凰台5A新考案高中数学二轮基础版》

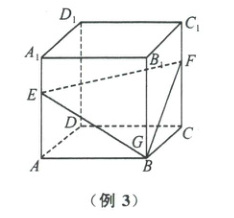
例 3 (2025·茂名一模)如图,在棱长为 6 的正方体 $ABCD - A_{1}B_{1}C_{1}D_{1}$ 中,$\overrightarrow{AE}=2\overrightarrow{EA_{1}}$,$\overrightarrow{CF}=2\overrightarrow{FC_{1}}$,过点 $B,E,F$ 的平面截该正方体所得截面的周长为(B)


A.$4\sqrt{13}+3\sqrt{2}$
B.$6\sqrt{13}+3\sqrt{2}$
C.$4\sqrt{13}+8\sqrt{2}$
D.$6\sqrt{13}+8\sqrt{2}$

答案：
例3　B[解析]如图，取D₁C₁的中点N，D₁A₁的中点M，连接MN，NF，ME，则五边形BEMNF为过点B，E，F的截面，取CF的中点J，DD₁靠近D₁的三等分点K，连接D₁J，CK，EK，则NF//D₁J。又CJ//D₁K且CJ = D₁K，所以四边形CJD₁K为平行四边形，所以CK//D₁J，则NF//CK。又EK//BC且EK = BC，所以四边形EKCB为平行四边形，所以EB//CK，则NF//BE，所以N，F，B，E四点共面。分别取BB₁，AA₁靠近B，A的三等分点G，H，连接C₁G，GH，D₁H，同理可证BF//C₁G，D₁H//C₁G，D₁H//EM，所以BF//EM，所以B，F，M，E四点共面，所以N，F，B，E，M五点共面。又NF = ME = $\sqrt{2² + 3²}$ = $\sqrt{13}$，BE = BF = $\sqrt{4² + 6²}$ = 2$\sqrt{13}$，MN = $\sqrt{3² + 3²}$ = 3$\sqrt{2}$，所以截面的周长为6$\sqrt{13}$ + 3$\sqrt{2}$。

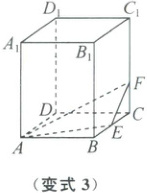
变式 3 如图,在直四棱柱 $ABCD - A_{1}B_{1}C_{1}D_{1}$ 中,底面 $ABCD$ 是边长为 2 的正方形,侧棱 $AA_{1}=3$,$E$ 是 $BC$ 的中点,$F$ 是棱 $CC_{1}$ 上的点,且 $CF=\frac{1}{3}CC_{1}$,过 $A_{1}$ 作平面 $\alpha$,使得平面 $\alpha//$ 平面 $AEF$,则平面 $\alpha$ 截直四棱柱 $ABCD - A_{1}B_{1}C_{1}D_{1}$ 所得截面图形的面积为(A)


A.$\frac{3}{2}$
B.$\frac{\sqrt{19}}{2}$
C.$3$
D.$\sqrt{19}$

答案：
变式3　A　[解析]如图，取B₁C₁的中点M，在BB₁上取一点H，使得B₁H = $\frac{1}{3}$BB₁，连接A₁M，HM，A₁H，则A₁M//AE，HM//EF，可证得平面AEF//平面A₁HM，即过点A₁平行于平面AEF的平面截四棱柱ABCD - A₁B₁C₁D₁所得图形是△A₁HM，其中B₁H = $\frac{1}{3}$BB₁ = 1，A₁H = $\sqrt{5}$，A₁M = $\sqrt{5}$，MH = $\sqrt{2}$，则cos∠MA₁H = $\frac{A₁M² + A₁H² - MH²}{2A₁M · A₁H}$ = $\frac{4}{5}$，所以sin∠MA₁H = $\frac{3}{5}$，从而S△A₁MH = $\frac{1}{2}$A₁M · A₁H · sin∠MA₁H = $\frac{1}{2} × \sqrt{5} × \sqrt{5} × \frac{3}{5} = \frac{3}{2}$。

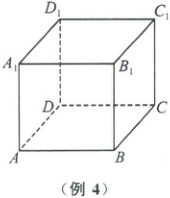
例 4 (2025·九江一模)如图,在棱长为 $\sqrt{3}$ 的正方体 $ABCD - A_{1}B_{1}C_{1}D_{1}$ 中,点 $P$ 在正方体内(包含边界)运动.若直线 $A_{1}P$ 与 $DC$ 所成的角为 $\frac{\pi}{6}$,则动点 $P$ 所围成的图形的面积是(B)


A.$\frac{\pi}{4}$
B.$\frac{\pi}{2}$
C.$\frac{3\pi}{4}$
D.$\pi$

答案：
例4　B　[解析]如图，在正方体ABCD - A₁B₁C₁D₁中，DC//A₁B₁。由直线A₁P与DC所成的角为$\frac{\pi}{6}$，知直线A₁P与直线A₁B₁所成的角为$\frac{\pi}{6}$，故动点P所围成的图形是高为$\sqrt{3}$，底面半径为1，母线长为2的圆锥侧面的四分之一，即动点P所围成的图形的面积为$\frac{1}{4}$×π×1×2 = $\frac{\pi}{2}$。

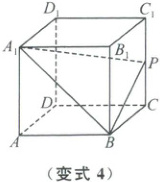
变式 4 (2025·徐州 2 月调研节选)如图,在直四棱柱 $ABCD - A_{1}B_{1}C_{1}D_{1}$ 中,底面 $ABCD$ 为菱形,$\angle BAD = 60^{\circ}$,$AB = AA_{1}=2$,$P$ 为 $CC_{1}$ 的中点,点 $Q$ 满足 $\overrightarrow{DQ}=\lambda\overrightarrow{DC}+\mu\overrightarrow{DD_{1}}(\lambda\in[0,1],\mu\in[0,1])$,且 $A_{1}Q=\sqrt{5}$,则点 $Q$ 的轨迹长度为$\frac{\sqrt{2}\pi}{4}$.

答案：
变式4　$\frac{\sqrt{2}\pi}{4}$　[解析]如图，取AB的中点R，因为底面ABCD为菱形，∠BAD = 60°，故DR⊥DC。以D为原点，以DR，DC，DD₁分别为x，y，z轴，建立空间直角坐标系，则A₁($\sqrt{3}$， - 1，2)，可得Q(0，2λ，2μ)，则|A₁Q| = $\sqrt{(\sqrt{3})² + (2λ + 1)² + (2μ - 2)²}$ = $\sqrt{5}$，化简得(2λ + 1)² + (2μ - 2)² = 2，点Q满足$\overrightarrow{DQ} = \lambda\overrightarrow{DC} + \mu\overrightarrow{DD₁}$(λ∈[0, 1]，μ∈[0, 1])，即点Q在正方形CDD₁C₁内，包括边界，故点Q的轨迹为以S(-$\frac{1}{2}$，1)为圆心，$\frac{\sqrt{2}}{2}$为半径的圆，落在正方形CDD₁C₁内的部分如图所示。因为SH = $\frac{\sqrt{2}}{2}$，SD₁ = $\frac{1}{2}$，故DH = $\sqrt{(\frac{\sqrt{2}}{2})² - (\frac{1}{2})²}$ = $\frac{1}{2}$，故△SD₁H为等腰直角三角形，∠D₁SH = $\frac{\pi}{4}$，故点Q的轨迹长度为$\frac{\pi}{4}$×$\sqrt{2}$ = $\frac{\sqrt{2}\pi}{4}$。