《2026年南方凤凰台5A新考案高中数学二轮基础版》

1. (人A选必三P59例1改编)设某项试验的成功率是失败率的2倍，用随机变量$\xi$表示一次试验的成功次数，则$P(\xi = 0)=$(B)

A.0
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$

答案： 1.B【解析】设$P(\xi=1)=p$，则$P(\xi=0)=1-p$．依题意知，$p=2(1-p)$，解得$p=\frac{2}{3}$，故$P(\xi=0)=1-p=\frac{1}{3}$．

2. 已知$X$的分布列为

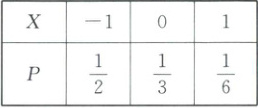
设$Y = 2X + 3$，则$E(Y)$的值为(A)

A.$\frac{7}{3}$
B.4
C.$-1$
D.1

答案： 2.A【解析】$E(X)=-\frac{1}{2}+\frac{1}{6}=-\frac{1}{3}$，$E(Y)=E(2X+3)=2E(X)+3=-\frac{2}{3}+3=\frac{7}{3}$．

3. 有甲、乙两种水稻，测得每种水稻各10株的分蘖数据，计算出样本均值$E(X_{甲})=E(X_{乙})$，方差分别为$D(X_{甲})=11$，$D(X_{乙})=3.4$。由此可以估计(B)

A.甲种水稻比乙种水稻分蘖整齐
B.乙种水稻比甲种水稻分蘖整齐
C.甲、乙两种水稻分蘖整齐程度相同
D.甲、乙两种水稻分蘖整齐程度不能比较

答案： 3.B

4. 设$0 ＜ m ＜ 1$，随机变量$\xi$的分布列为

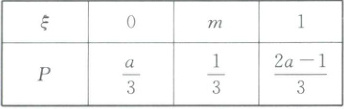
则当$m$在$(0,1)$上增大时，(D)

A.$D(\xi)$单调递增，最大值为$\frac{1}{2}$
B.$D(\xi)$先增后减，最大值为$\frac{1}{3}$
C.$D(\xi)$单调递减，最小值为$\frac{2}{9}$
D.$D(\xi)$先减后增，最小值为$\frac{1}{6}$

答案： 4.D【解析】由题知$\frac{a}{3}+\frac{1}{3}+\frac{2a-1}{3}=1$，解得$a=1$，所以$E(\xi)=0+\frac{m}{3}+\frac{1}{3}=\frac{m+1}{3}$，所以$D(\xi)=(0-\frac{m+1}{3})^2×\frac{1}{3}+(m-\frac{m+1}{3})^2×\frac{1}{3}+(1-\frac{m+1}{3})^2×\frac{1}{3}=\frac{2}{9}(m^2-m+1)=\frac{2}{9}[(m-\frac{1}{2})^2+\frac{3}{4}]$．由二次函数性质可知，$D(\xi)$在$(0,\frac{1}{2})$上单调递减，在$(\frac{1}{2},1)$上单调递增，所以当$m=\frac{1}{2}$时，$D(\xi)$取最小值$\frac{1}{6}$．

5. 为了调查公司员工的健康状况，用分层随机抽样的方法抽取样本，若样本中有20名男员工，30名女员工，且男员工的平均体重为70kg，标准差为4，女员工的平均体重为50kg，标准差为6，则所抽取样本的方差为124。

答案： 5.124【解析】由题意知，样本的平均数$\bar{x}=\frac{20×70+30×50}{20+30}=58$，样本的方差$s^2=\frac{20}{20+30}[4^2+(58-70)^2]+\frac{30}{20+30}[6^2+(58-50)^2]=124$．