《2026年南方凤凰台5A新考案高中数学二轮基础版》

例3 (2025·南昌二模)为宣扬中国文化,某校组织古诗词知识比赛,比赛分为两阶段,第一阶段为基础知识问答,每位选手都需要回答3个问题,答对其中至少2个问题,进入第二阶段,否则被淘汰.第二阶段分高分组和低分组,第一阶段3个问题都答对的选手进入高分组,共回答4个问题,每答对一个得20分,答错不得分;第一阶段答对2个问题的选手进入低分组,共回答4个问题,每答对一个得10分,答错不得分.第一阶段,每个问题选手甲答对的概率都是$\frac{2}{3}$;第二阶段,若选手甲进入高分组,则每个问题答对的概率都是$\frac{1}{4}$,若选手甲进入低分组,则每个问题答对的概率都是$\frac{1}{2}$.
(1)求选手甲第一阶段不被淘汰的概率;
(2)求选手甲在该次比赛得分为40分的概率;
(3)已知该次比赛选手甲进入了高分组,记选手甲在该次比赛中得分为$X$,求随机变量$X$的分布列和数字期望.

答案：
例3【解答】
(1)选手甲第一阶段不被淘汰，即甲回答3个问题答对其中2个或3个，其概率为$p_1 = C_{3}^{2}(\frac{2}{3})^{2} × \frac{1}{3} + (\frac{2}{3})^{3} = \frac{20}{27}$。
(2)选手甲在该次比赛得分为40分有两种情况：进入高分组，答对2个问题；进入低分组，答对4个问题。所求概率为$p_2 = C_{3}^{2}(\frac{2}{3})^{2} × \frac{1}{3} × (\frac{1}{2}) + (\frac{2}{3})C_{4}^{3}(\frac{3}{4})^{3} × (\frac{1}{4}) = \frac{13}{144}$。
(3)$X$的可能取值有0,20,40,60,80，$P(X = 0) = C_{4}^{3}(\frac{3}{4})^{3} = \frac{81}{256}$，$P(X = 20) = C_{4}^{3}(\frac{3}{4})^{2} × \frac{1}{4} = \frac{108}{256}$，$P(X = 40) = \frac{108}{256}$，$P(X = 60) = C_{4}^{2}(\frac{3}{4})^{2} × (\frac{1}{4})^{2} = \frac{54}{256}$，$P(X = 80) = C_{4}^{4}(\frac{1}{4})^{4} = \frac{1}{256}$，所以$X$的分布列为

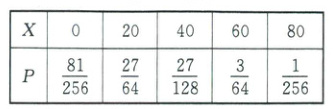
所以$E(X) = 20 × 4 × \frac{1}{4} = 20$。