2026年南方凤凰台5A新考案高中数学二轮基础版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年南方凤凰台5A新考案高中数学二轮基础版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
例 3 在电子制造业高质量发展的大环境下,某企业统筹各类资源,进行了积极的改革探索。下表是该企业每月生产的一种核心产品的产量 $ x(3\leq x\leq15) $(单位:件)与相应的生产总成本 $ y $(单位:万元)的四组对照数据。

企业研究人员建立了 $ y $ 关于 $ x $ 的两种回归模型,利用计算得到如下经验回归方程:
① $ \hat{y}_{1}=\frac{x^{3}}{3} + 173 $;② $ \hat{y}_{2}=68x - 160 $。其中经验回归方程①的残差图如图所示(残差 = 观测值 - 预测值)。
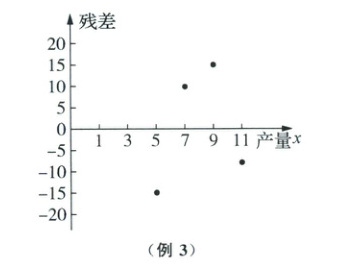
(1)在下表中填写经验回归方程②的残差,根据残差分析,判断哪一个经验回归方程更适宜作为 $ y $ 关于 $ x $ 的回归方程,并说明理由。
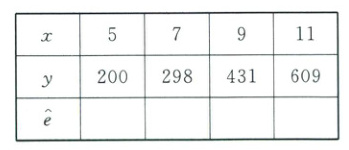
(2)从该企业过去几年生产的该产品中随机抽取 100 件,其中优等品有 60 件,合格品有 40 件。每件优等品利润为 20 万元,每件合格品利润为 15 万元。若以频率估计概率,该企业某月计划生产 12 件该产品,记优等品件数为 $ X $,总利润为 $ Y $。
①求 $ Y $ 与 $ X $ 的关系式,并求 $ E(X) $ 和 $ E(Y) $;
②记该月的成本利润率为 $ p $,在(1)中选择的经验回归方程下求 $ p $ 的估计值。(结果保留 2 位小数)
附:成本利润率 $ = \frac{总利润}{总成本}$

企业研究人员建立了 $ y $ 关于 $ x $ 的两种回归模型,利用计算得到如下经验回归方程:
① $ \hat{y}_{1}=\frac{x^{3}}{3} + 173 $;② $ \hat{y}_{2}=68x - 160 $。其中经验回归方程①的残差图如图所示(残差 = 观测值 - 预测值)。

(1)在下表中填写经验回归方程②的残差,根据残差分析,判断哪一个经验回归方程更适宜作为 $ y $ 关于 $ x $ 的回归方程,并说明理由。

(2)从该企业过去几年生产的该产品中随机抽取 100 件,其中优等品有 60 件,合格品有 40 件。每件优等品利润为 20 万元,每件合格品利润为 15 万元。若以频率估计概率,该企业某月计划生产 12 件该产品,记优等品件数为 $ X $,总利润为 $ Y $。
①求 $ Y $ 与 $ X $ 的关系式,并求 $ E(X) $ 和 $ E(Y) $;
②记该月的成本利润率为 $ p $,在(1)中选择的经验回归方程下求 $ p $ 的估计值。(结果保留 2 位小数)
附:成本利润率 $ = \frac{总利润}{总成本}$
20
。-18
-21
答案:
例3 [解答]
(1)经验回归方程②的残差数据如下表:
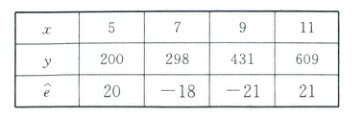
经验回归方程②的残差图如图所示。
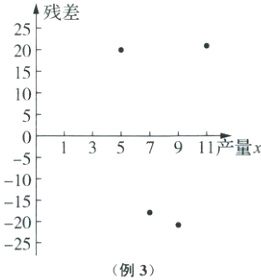
经验回归方程①更适宜作为$y$关于$x$的经验回归方程(以下理由或其他合理的理由,说出一条即可)。理由1:经验回归方程①的4个样本点的残差的绝对值都比经验回归方程②的小。理由2:经验回归方程①的4个样本的残差点落在的带状区域比经验回归方程②的带状区域更窄。理由3:经验回归方程①的4个样本的残差点比经验回归方程②的残差点更贴近$x$轴。
(2)①由题意知,每件产品为优等品的概率$P_0=\frac{60}{100}=0.6$,则$X\sim B(12,0.6)$,因此$E(X)=12×0.6 = 7.2$。由$Y = 20X + 15×(12 - X)=5X + 180$,得$E(Y)=5E(X)+180 = 216$(万元)。
②由①知总利润为216万元,总成本估计值$\hat{y}_1=\frac{12^3}{3}+173 = 749$(万元),则$p=\frac{216}{749}\approx0.29$。
例3 [解答]
(1)经验回归方程②的残差数据如下表:

经验回归方程②的残差图如图所示。

经验回归方程①更适宜作为$y$关于$x$的经验回归方程(以下理由或其他合理的理由,说出一条即可)。理由1:经验回归方程①的4个样本点的残差的绝对值都比经验回归方程②的小。理由2:经验回归方程①的4个样本的残差点落在的带状区域比经验回归方程②的带状区域更窄。理由3:经验回归方程①的4个样本的残差点比经验回归方程②的残差点更贴近$x$轴。
(2)①由题意知,每件产品为优等品的概率$P_0=\frac{60}{100}=0.6$,则$X\sim B(12,0.6)$,因此$E(X)=12×0.6 = 7.2$。由$Y = 20X + 15×(12 - X)=5X + 180$,得$E(Y)=5E(X)+180 = 216$(万元)。
②由①知总利润为216万元,总成本估计值$\hat{y}_1=\frac{12^3}{3}+173 = 749$(万元),则$p=\frac{216}{749}\approx0.29$。
查看更多完整答案,请扫码查看


