《2025年初中同步练习册七年级数学上册鲁教版54制北京师范大学出版社》

8. 设边长为$3的正方形的对角线长为a$,给出下列四种说法：①$a$是一个无理数；②$a$可以用数轴上的一个点来表示；③$3\lt a\lt4$；④$a是18$的算术平方根。其中正确的是①②④。(填序号)

答案： ①②④

9. 已知$2x + 1的平方根是\pm5$,则$5x + 4$的立方根是4。

答案： 4

10. 若$a$,$b$均为正整数,且$a\gt\sqrt{7}$,$b\lt\sqrt[3]{10}$,则$a + b$的最小值是4。

答案： 4

11. 将下列各数填入相应的集合内：
$-7$,$0.32$,$\frac{1}{3}$,$0$,$-\pi$,$2.\dot{1}\dot{6}$,$(\pi - 2)^{0}$,$5$,$0.1010010001…$(相邻两个$1之间0的个数逐次加1$)。
①有理数集合…$\{\}$；
②无理数集合…$\{\}$；
③负实数集合…$\{\}$。

答案： ①$-7,0.32,\frac{1}{3},0,2.\dot{1}\dot{6},(\pi - 2)^0,5$
②$-\pi,0.1010010001\cdots$(相邻两个1之间0的个数逐次加1)
③$-7,-\pi$

12. 求下列各式的值。
(1)$3\sqrt{2}-3\sqrt{3}+10\sqrt{3}-3\sqrt{2}$；
(2)$0.5-\sqrt{\frac{49}{16}}+\sqrt[3]{-\frac{1}{64}}$。

答案： 解:
(1)原式$=3\sqrt{2}-3\sqrt{2}+10\sqrt{3}-3\sqrt{3}=7\sqrt{3}$。
(2)原式$=0.5-\frac{7}{4}+(-\frac{1}{4})=-\frac{3}{2}$。

13. 求下列各式中$x$的值：
(1)$x^{2}-81 = 0$；
(2)$3(x + 1)^{2}-1 = 8$；
(3)$x^{3}+125 = 0$；
(4)$-8(x - 3)^{3}= 27$。

答案： 解:
(1)$x=\pm 9$
(2)$x=\pm \sqrt{3}-1$
(3)$x=-5$
(4)$x=\frac{3}{2}$

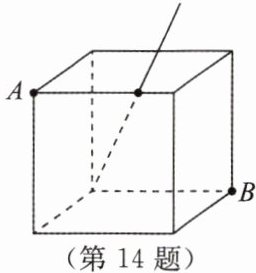
14. 已知正方体纸盒的表面积为$12\mathrm{cm}^{2}$。
(1)求正方体的棱长。
(2)拿掉盒盖后,插入一根长为$5\mathrm{cm}$的细木棒,则细木棒露在外面的长度最短是多少？
(3)一只蚂蚁在纸盒的表面由$A爬到B$,求蚂蚁爬行的最短路程是多少。

答案：
解:
(1)正方体有六个表面,每个面的面积为$2\ cm^2$,则棱长为$\sqrt{2}\ cm$。
(2)如图,插入细木棒后,要使细木棒露在外面的长度最短,则看不见的部分应恰好是正方体的对角线$CE$,$CD=\sqrt{(\sqrt{2})^2+(\sqrt{2})^2}=\sqrt{4}=2(cm)$,$CE=\sqrt{2^2+(\sqrt{2})^2}=\sqrt{6}(cm)$,则露在外面的长度最短为$(5 - \sqrt{6})\ cm$。
(3)如图,要算立体图形上两点之间的最短路程,首先需要将其转化成平面图形,将$EB$所在的面绕$DE$顺时针旋转$90°$,与$AD$所在平面重合,即可计算$AB'$之间的距离,$AB'=\sqrt{(\sqrt{8})^2+(\sqrt{2})^2}=\sqrt{10}(cm)$,因此,蚂蚁爬行的最短路线长$\sqrt{10}\ cm$。