《2025年初中同步练习册七年级数学上册鲁教版54制北京师范大学出版社》

6. 某直角三角形的两直角边分别长$3和4$,则斜边上的高为2.4。

答案： 2.4

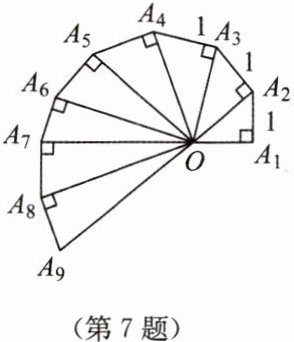
7. 如图所示的是第七届国际数学教育大会的会徽,它的主题图案是由一连串如图所示的直角三角形演化而成的。若其中第一个直角三角形$OA_{1}A_{2}$为等腰三角形,且$OA_{1}= A_{1}A_{2}= A_{2}A_{3}= A_{3}A_{4}=… =A_{8}A_{9}= 1$,则$OA_{9}$的长是3。

答案： 3

8. 在$\triangle ABC$中,$AB = 17$,$AC = 10$,$BC边上的高是8$,则$BC$的长是21或9。

答案： 21或9

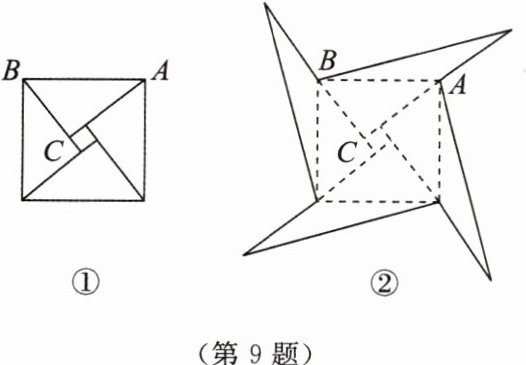
9. 图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的。若$AC = 6$,$BC = 5$,将四个直角三角形中边长为$6$的直角边分别向外延长一倍,得到如图②所示的“数学风车”,则这个风车的外围周长是76。

答案： 76

10. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC + BC = 15$,$AB = 11$,则$Rt\triangle ABC$的面积为26。

答案： 26

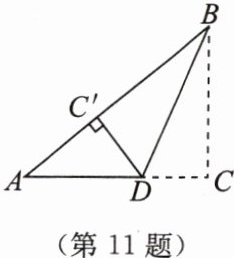
11. 如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$BC = 6cm$,$AC = 8cm$,按图中所示方法将$\triangle ABC沿BD$折叠,使点$C落在AB边的点C'$处,求$\triangle ADC'$的面积。

答案： $6\ cm^{2}$

12. 如图,圆柱形玻璃杯高为$12cm$,底面周长为$18cm$,在杯内离杯底$4cm的点C$处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿$4cm与蜂蜜相对的点A$处,则蚂蚁到达蜂蜜处的最短路程为多少？

答案：
解:沿过点A的圆柱的高线剪开，得出长方形EFGH,过点C作$CQ\perp EF$于点Q,作点A关于EH的对称点$A'$,连接$A'C$交EH于点P,连接AP,则$AP+PC$就是蚂蚁到达蜂蜜处的最短距离。
　　因为$AE=A'E$,$A'P=AP$,
　　所以$AP+PC=A'P+PC=A'C$。
　　又因为$CQ=\frac{1}{2}×18=9(cm)$,
　　$A'Q=12 - 4 + 4 = 12(cm)$,
　　所以在$Rt\triangle A'QC$中,由勾股定理可得,
　　
　　$A'C^{2}=9^{2}+12^{2}=225$,
　　所以$A'C = 15\ cm$。
　　因此蚂蚁到达蜂蜜处的最短路程为$15\ cm$。

13. 台风是一种自然灾害,有极强的破坏力。如图,台风中心沿东西方向由点$A向点B$移动,已知点$C$为一海港,且$AC = 300km$,$BC = 400km$,$AB = 500km$,台风中心的移动速度为$25km/h$。经测量,距离台风中心$260km$及以内的地区会受到影响。海港$C$会受到台风影响吗？若会受到台风影响,请求出受影响的时间有多长；若不会受到台风影响,请说明理由。

答案：
解:如图，过点C作$CD\perp AB$于点D。因为$AC = 300\ km$,$BC = 400\ km$,$AB = 500\ km$,
　　所以$AC^{2}+BC^{2}=300^{2}+400^{2}=500^{2}=AB^{2}$,所以$\triangle ABC$为直角三角形，且$\angle ACB = 90^{\circ}$,所以$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD=\frac{1}{2}AC\cdot BC$,
　　所以$500CD = 300×400$，所以$CD = 240\ km$。
　　因为$240\ km＜260\ km$,
　　所以海港C会受到台风影响。
　　如图，在线段AB上找到点E,F，使$DE = DF$,连接EC,FC。
　　
　　因为$DE = DF$,$CD\perp AB$,
　　所以$EC = FC$。
　　当$EC = FC = 260\ km$时,台风正好影响海港C。
　　在$Rt\triangle CED$中,由勾股定理得$CD^{2}+ED^{2}=CE^{2}$,
　　即$240^{2}+ED^{2}=260^{2}$,
　　所以$ED = 100\ km$。
　　因为$DE = DF = 100\ km$,
　　所以$EF = 2DE = 200\ km$。
　　因为台风中心的移动速度为$25\ km/h$,
　　所以$200÷25 = 8(h)$，
　　即海港C受影响的时间为$8\ h$。